На этом шаге мы рассмотрим последний пример использования топологической сортировки.
Лемма [1, с.127].
В произвольном ориентированном бесконтурном графе вершины можно перенумеровать так, что каждая дуга будет иметь вид (vi,vj), где i<j.
Для доказательства леммы предложим алгоритм, конструирующий такую нумерацию (в виде программы на языке С++).
Алгоритм основывается на следующем простом факте: в произвольном бесконтурном графе существует вершина, в которую не заходит ни одна дуга.
Чтобы убедиться в этом, выберем произвольную вершину w1 графа, затем некоторую вершину w2, такую что w1<-w2, и т.д. Через конечное число шагов мы должны дойти до некоторой вершины wi, в которую не заходит ни одна дуга, ибо в силу бесконтурности ни одна вершина не может повторяться в последовательности w1,w2,w3,...
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; // Нумерация вершин в бесконтурном графе. typedef struct Leader *Lref; //Тип: указатель на заголовочный узел. typedef struct Trailer *Tref; //Тип: указатель на дуговой узел. //Описание типа заголовочного узла. struct Leader { int Key; //Имя заголовочного узла. int Number; //Новый номер вершины. int Count; //Количество предшественников. int Count1; //Количество последующих вершин. Tref Pred; //Указатель на список предшественников. Tref Trail; //Указатель на список последователей. Lref Next; //Указатель на следующий узел в //списке заголовочных узлов. }; //Описание типа дугового узла. struct Trailer { Lref Id; Tref Next; }; //Описание типа узла стека. struct Zveno { Lref Element; //Указатель на вершину. Zveno* Sled; }; class Spisok { private: Lref Head; //Указатель на список заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент //в конце списка заголовочных узлов. Zveno* Stack; //Указатель на рабочий стек. Lref SearchGraph (int); void Udalenie (Lref*); void V_Stack (Lref); public: Spisok () {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); }; void MakeGraph(); void PrintGraph(); void Renum(); void Vyvod(); }; void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? p=SearchGraph (x); q=SearchGraph (y); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; t = new (Trailer); (*t).Id = p; (*t).Next = (*q).Pred; (*q).Pred = t; (*p).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } Lref Spisok::SearchGraph (int w) //Функция возвращает указатель на заголовочный узел //с ключом w. Если заголовочный узел отсутствует, то он //добавляется в список. Head - указатель на структуру Вирта. { Lref h; h = Head; (*Tail).Key = w; while ((*h).Key!=w) h = (*h).Next; if (h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (Leader); (*h).Count = (*h).Count1 = 0; (*h).Trail = (*h).Pred = NULL; (*h).Next = Tail; } return h; } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<(*p).Key<<"(("; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key<<" "; q = (*q).Next; } cout<<")("; q = p->Pred; while (q!=NULL) { cout << (*(*q).Id).Key<<" "; q = q->Next; } cout << "))"; p = (*p).Next; cout<<" "; } } void Spisok::Vyvod() { Lref p = Head; while ( p!=Tail ) { cout << p->Key << '-'<< p->Number; p = p->Next; cout << ' '; } } void Spisok::Renum() //Перенумерация вершин графа, заданного структурой Вирта //с указателем Head. { int num; Lref p,u; Tref t; Stack = NULL; p = Head; while ( p!=Tail ) { if ( p->Count!=0 ) V_Stack(p); p = p->Next; } num = 0; while ( Stack!=NULL ) { Udalenie (&u); num++; u->Number = num; t = u->Trail; while ( t!=NULL ) { t->Id->Count--; if ( t->Id->Count==0 ) V_Stack (t->Id); t = t->Next; } } } void Spisok::Udalenie (Lref *Klad) // Удаление элемента из стека Stack и сохранение его в // переменной Klad. { Zveno *q; if ( Stack==NULL ) cout << "Ошибка! Попытка выбоpа из пустого стека!\n"; else { (*Klad) = Stack->Element; q = Stack; Stack = Stack->Sled; delete q; } } void Spisok::V_Stack (Lref Elem) // Помещение Elem в стек Stack. { Zveno *q; q = new (Zveno); q->Element = Elem; q->Sled = Stack; Stack = q; } void main() { Spisok A; // Построение графа и вывод его структуры смежности. A.MakeGraph(); A.PrintGraph(); cout << endl; A.Renum(); // Вывод новых номеров вершин графа. A.Vyvod(); }
Результат работы программы изображен на рисунке 1:
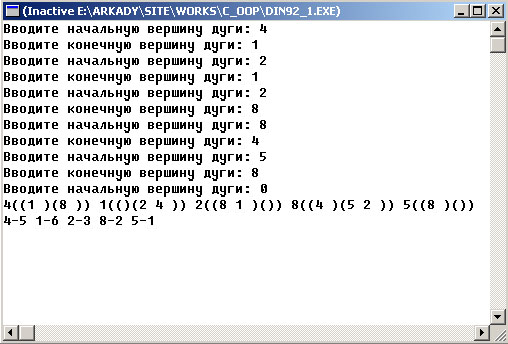
Рис.1. Результат работы приложения
(1) Липский В. Комбинаторика для программистов: Пер. с польск. - М.:Мир, 1988. - 213 с.
На следующем шаге мы дадим понятие о методе PERT.
