На этом шаге мы приведем последний пример использования топологической сортировки.

Сетевое планирование - совокупность методов, использующих сетевую модель как основную форму представления информации об управляемом комплексе работ. Использование сетевого планирования позволяет повысить качетсво планирования и управления при реализации комплекса работ, например, дает возможность четко координировать деятельность всех сторон (организаций), участвующих в реализации, выделять наиболее важные задачи, определять сроки реализации, а также координировать план его реализации [1, с.540].

Сетевая модель - информационная модель реализации некоторого комплекса взаимосвязанных работ, рассматриваемая как ориентированный граф без контуров, отображающий естественный порядок выполнения этих работ во времени; может содержать некоторые дополнительные характеристики (например, время, стоимость, ресурсы), относящиеся к отдельным работам и (или) к комплексу в целом.

Наибольшее распространение получило графическое представление сетевой модели на плоскости, называемое сетевым графиком [1, с.540].

Для быстрого "погружения" в постановку и решение задач сетевого планирования рассмотрим простейший пример, заимствованный нами из монографий [2; 3, с.409].

Предположим, что шеф-повар получил заказ приготовить яичницу из одного яйца. Вся процедура ее приготовления может быть разбита на ряд отдельных подзадач:

   Взять яйцо ----> Разбить яйцо ----> Взять жир ---->
   ----> Положить жир на сковороду ----> Растопить жир ---->
   ----> Вылить яйцо на сковороду ---->
   ----> Ждать, пока яичница не изжарится ----> Снять яичницу

Некоторые из этих подзадач должны предшествовать другим (например, задача "взять яйцо" должна предшествовать задаче "разбить яйцо"). Ряд подзадач может выполняться параллельно (например, задачи "взять яйцо" и "растопить жир"). Шеф-повар хотел бы выполнить заказ как можно быстрее, при этом предполагается, что число его помощников не ограничено.

Необходимо распределить работу среди помощников так, чтобы заказ был выполнен за минимально возможное время.

Хотя этот пример может показаться легкомысленным, подобная задача возникает во многих ситуациях, связанных с планированием реальных действий. В больших вычислительных системах осуществляется планирование заданий с целью обеспечения минимального времени нахождения задания в системе, технолог на заводе может планировать организацию работы конвейера, минимизирующую время производства продукции, и т.п. Все проблемы подобного рода тесно связаны между собой и могут быть решены с использованием графов.

Давайте представим исходную задачу в виде графа. Каждая вершина графа представляет собой подзадачу, а каждая дуга (x,y) представляет требование, что задача y не может выполняться до тех пор, пока не завершено выполнение задачи x. Граф задачи показан на рисунке:

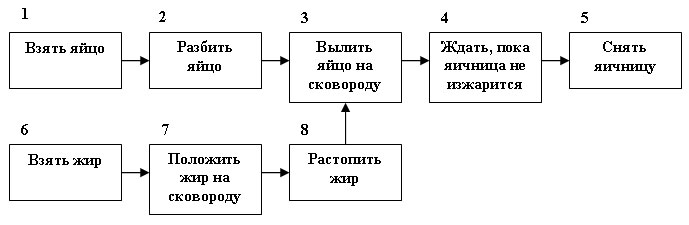
Рис.1. Граф задачи

Заметим, что в изображенном графе узлы 1 и 6 не имеют предшественников, и, следовательно, подзадачи, которые они представляют, могут выполняться сразу же и параллельно без ожидания завершения других подзадач. Все остальные подзадачи должны ждать завершения по крайней мере одной из этих подзадач. Как только эти первые две подзадачи завершены, соответствующие вершины и инцидентные дуги могут быть удалены из графа. Отметим, что получающийся в результате граф не содержит контуров, поскольку вершины и дуги удалялись из графа без циклов. Стало быть, новый граф также должен содержать по крайней мере один узел, не имеющий предшественников. В нашем примере существуют два таких узла - 2 и 7. Значит, подзадачи 2 и 7 могут выполняться параллельно во второй период времени.

Продолжив построение далее, мы найдем, что минимальное время, за которое может быть поджарена яичница, - шесть временных периодов (предполагая, что каждая подзадача требует ровно один период времени), а максимальное требующееся число помощников - два:

 Период времени         Помощник 1                 Помощник 2       
                                                      
      1                 Взять яйцо                 Взять жир                 
      2                 Разбить яйцо               Положить жир на сковороду 
      3                 Растопить жир            
      4                 Вылить яйцо на сковороду 
      5                 Ждать, пока яичница не изжарится   
      6                 Снять яичницу

Автоматизируем процесс построения решения задачи, модифицируя алгоритм топологической сортировки, проиллюстрированный программой из 89 шага, следующим образом:

   while  (Граф не пуст)
     {
        Определить вершины, не имеющие предшественников.
        Распечатать эту  группу  узлов с указанием,  что эти подзадачи
        могут быть выполнены параллельно в следующий  момент  времени.
        Удалить из графа данные вершины и инцидентные дуги
     }

Программа. Применение топологической сортировки для решения простейших задач сетевого планирования.

#include <iostream.h>
typedef struct Leader  *Lref; //Тип: указатель на заголовочный узел.
typedef struct Trailer *Tref; //Тип: указатель на дуговой узел.
//Описание типа заголовочного узла.
typedef struct Leader 
{
  int Key;    //Информационное поле.
  int Count;  //Количество предшественников.
  Tref Trail; 
  Lref Next;  
};

//Описание типа дугового узла.
typedef struct Trailer 
{
  Lref Id; 
  Tref Next; 
};

class Spisok {
  private:
    Lref Head; //Указатель на список заголовочных узлов.
    Lref Tail; //Указатель на фиктивный элемент 
               //в конце списка заголовочных узлов.
    int z;     //Количество узлов, не имеющих предшественников.
  public:
    Spisok () {//Инициализация списка заголовочных узлов.
               Head = Tail = new (Leader); z = 0;};
    Lref L (int); 
    void Poisk();
    void Vyvod();
};

void Spisok::Poisk()
{
  Lref p,q; // Рабочие указатели.
  
  p = Head; Head = NULL;
  while (p!=Tail)
  {
     q = p; p = p->Next;
     if (q->Count==0)
       { q->Next = Head; Head = q; }
   }
}

Lref Spisok::L (int w) 
//Функция возвращает указатель на ведущего с ключом w.
{
  Lref h = Head;

  Tail->Key = w;
  while (h->Key!=w) h = h->Next;
  if (h==Tail)
  // В списке нет элемента с ключом w.
  {
    Tail = new (Leader); z++;
    h->Count = 0; h->Trail = NULL; h->Next = Tail;
  }
  return h;
}

void Spisok::Vyvod()
{
  Lref p,q; // Рабочие указатели.
  Lref S,U; // Рабочие указатели.
  Tref t;
  
  cout << endl;
  cout << "Результат...\n";
  q = Head;
  while ( q!=NULL) 
  // Вывод всех элементов с нулевым количеством предшественников.
  {
     S = q; cout << "( ";
     while ( S!=NULL )
     {  cout << S->Key << " "; z--; S = S->Next;  }
     cout << ") ";
     // --------------------------------------------------- 
     U = NULL; // Указатель на очередной список элементов 
               // с нулевым количеством предшественников.
     while ( q!=NULL )
     {
       t = q->Trail;
       while ( t!=NULL )
       {
         p = t->Id; p->Count--;
         if ( p->Count==0 ) // Включение (*p) в список ведущих.
            { p->Next = U; U = p; }
         t = t->Next;
       }
       q = q->Next;
     }
     q = U;
  }
  if (z!=0)
      cout << "\nМножество не является частично упорядоченным!\n";
}

void main()
{
  Spisok A;
  Lref p,q; // Рабочие указатели.
  Tref t;
  int  x,y; // Рабочие переменные.

  // Фаза ввода.
  cout << "Задайте отношение частичного порядка...\n";
  cout << "Элемент "; 
  cin >> x; 
  cout << " предшествует элементу ";
  while (x!=0)
  {
    cin >> y;
    p = A.L(x); q = A.L(y);
    t = new (Trailer); t->Id = q; t->Next = p->Trail;
    p->Trail = t; q->Count += 1;
    cout << "Элемент "; 
    cin >> x;
    cout << " предшествует элементу ";
  }
  // Поиск ведущих с нулевым количеством предшественников.
  A.Poisk();
  // Фаза вывода.
  A.Vyvod();
}

Текст этой программы можно взять здесь.

Тестовые примеры:

Решением задачи планирования приготовления яичницы является:
```
    ( 6 1 ) ( 2 7 ) ( 8 ) ( 3 ) ( 4 ) ( 5 )
```

Решение задачи о топологическом упорядочении учебных курсов по математике, дискретной математике и информатике для студентов педагогических вузов (тестовый пример 3 из 89 шага) имеет следующий вид:

    ( 26 22 21 19 1 ) ( 3 4 6 24 17 20 ) ( 2 7 5 )
    ( 8 18 10 ) ( 9 11 25 ) ( 27 12 14 16 ) ( 13 15 23 )

Интерпретируя результаты, получим перечень блоков учебных курсов, которые можно преподавать параллельно:

   (Алгебра. Математический анализ.  Геометрия. Математическая логика.
Дискретная математика);
   (Теория автоматов.  Машинная арифметика. Теория графов. Реляционная
алгебра и реляционное исчисление.  Теория взаимодействующих последова-
тельных процессов. Теория алгоритмов);
   (Теория кодирования.  Формальные языки  и  грамматики.  Введение  в
программирование);
   (Структуры данных.  Устройство  ЭВМ.  Доказательство   правильности
программ);
   (Анализ алгоритмов. Компиляторы. Машинная графика);
   (Операционные системы.  Парадигмы программирования.  Информационный
поиск. Вычислительная геометрия);
   (Базы данных. Искусственный интеллект. Вычислительная математика).

    Замечание. Дискретная математика - область математики, занимающаяся изучением свойств дискретных структур, которые возникают как внутри математики, так и в ее приложениях. К числу таких структур могут быть отнесены, например, конечные группы, конечные графы, а также некоторые математические модели преобразователей информации, конечные автоматы, машины Тьюринга и т.д. Это примеры структур финитного (конечного) характера. Часть дискретной математики, изучающая их, называется конечной математикой. Иногда это понятие расширяют до дискретной математики. Помимо указанных финитных структур, дискретная математика изучает некоторые алгебраические системы, бесконечные графы, вычислительные схемы определенного вида, клеточные автоматы и т.д. [1, с.184].
    Наряду с выделением дискретной математики путем указания ее предмета можно также определить дискретную математику посредством перечисления подразделов, составляющих дискретную математику. К ним в первую очередь должны быть отнесены

комбинаторный анализ,
теория графов,
теория кодирования,
теория функциональных систем и некоторые другие (см.[4, 5, 6, 7, 8, 9]).

    Часто под термином "дискретная математика" (предполагая, что ее предмет исчерпывается конечными структурами) понимается именно совокупность перечисленных дисциплин.
    Мы будем понимать термин "дискретная математика" именно так и отнесем к ней следующие математические дисциплины:

машинную арифметику,
комбинаторный анализ,
теорию кодирования,
теорию графов,
теорию автоматов,
формальные языки и грамматики,
теорию взаимодействующих последовательных процессов.

Как отмечалось, возможно и более широкое толкование дискретной математики за счет расширения понимания ее предмета. С этой точки зрения к дискретной математике могут быть также отнесены как целые разделы математики, например, математическая логика, так и части таких разделов, как теория чисел, алгебра, вычислительная математика, теория вероятностей и другие, в которых изучаемый объект носит дискретный характер [1, с.184].

⁽¹⁾ Математический энциклопедический словарь. - М.: Сов.энциклопедия, 1988. - 847 с.
⁽²⁾ Tenenbaum A., Augenstein M. Data Structures Using Pascal. Englewood Cliffs. - N.Y.: Prentice-Hall, Inc. 1981.
⁽³⁾ Лэнгсам Й., Огенстейн М., Тененбаум А. Структуры данных для персональных ЭВМ: Пер. с англ. - М.: Мир, 1989. - 568 с.
⁽⁴⁾ Яблонский С.В. Введение в дискретную математику. - М.: Наука, 1986. - 384 с.
⁽⁵⁾ Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. - М.: Наука, 1977. - 368 с.
⁽⁶⁾ Горбатов В.А. Основы дискретной математики. - М.: Высш.шк., 1986. - 311 с.
⁽⁷⁾ Горбатов В.А. Дискретная математика в задачах и упражнениях. - М.: МГИ, 1988 (1989). - 100 с.
⁽⁸⁾ Триханов А.В. Основы дискретной математики. - Томск: ТПИ, 1987. - 96 с.
⁽⁹⁾ Задачи по дискретной математике. - Алма-Ата: КазГУ, 1986. - 30 с.

На следующем шаге мы рассмотрим способы представления грамматики.

Предыдущий шаг Содержание Следующий шаг