На этом шаге мы рассмотрим алгоритм обхода графа в глубину.
Обход в глубину (называемый иногда стандартным обходом), есть обход графа по следующим правилам:
- находясь в вершине x, нужно двигаться в любую другую, ранее не посещенную вершину (если таковая найдется), одновременно запоминая дугу, по которой мы впервые попали в данную вершину;
- если из вершины x мы не можем попасть в ранее не посещенную вершину или таковой вообще нет, то мы возвращаемся в вершину z, из которой впервые попали в x, и продолжаем обход в глубину из вершины z.
При выполнении обхода графа по этим правилам мы стремимся проникнуть "вглубь" графа так далеко, как это возможно, затем отступаем на шаг назад и снова стремимся пройти вперед и так далее.
На этом шаге мы приведем рекурсивную функцию обхода графа в глубину. Граф представлен в памяти структурой Вирта.
Заметим, что перед обращением к функции Depth_First_Search () необходимо провести инициализацию:
t = Head;
while (t!=Tail)
{(*t).Flag = TRUE; t = (*t).Next;}
Текст функции:
void Depth_First_Search (Lref r) { Tref t; t = (*r).Trail; cout<<(*r).Key; (*r).Flag = FALSE; while (t!=NULL) { if ((*(*t).Id).Flag) Depth_First_Search ((*t).Id); t = (*t).Next; } }
В связи с тем, что поиск в глубину играет важную роль в проектировании алгоритмов на графах, представим также нерекурсивную версию функции Depth_First_Search(), которую мы назовем Depth_First_Search_1().
В приведенной ниже формулировке нерекурсивного алгоритма поиска в глубину на графе [1,с.125-126] предполагается: во-первых, что зафиксирован некоторый линейный порядок на множестве всех вершин графа, и, во-вторых, что множество вершин, смежных со всякой вершиной графа, также линейно упорядочено.
while (Имеется хотя бы одна непосещенная вершина) { Пусть p - первая из непосещенных вершин. Посетить вершину p и поместить ее в пустой стек S; while ( Стек S непуст ) { Пусть p - вершина, находящаяся на верхушке стека S; if (У вершины p есть непосещенные смежные вершины) { Пусть q - первая непосещенная вершина из вершин, смежных вершине p. Пройти по ребру (p,q), посетить вершину q и поместить ее в стек S } else Удалить вершину p из стека S } }
Реализуем ту часть приведенного алгоритма, которая ограничивается обходом только одной связной компоненты графа (смотри шаг 78).
Не забудьте про предварительную инициализацию:
t = Head;
while (t!=Tail)
{ (*t).Flag = TRUE; t = (*t).Next; }
Текст функции:
void Depth_First_Search_1 (Lref r) { Tref t; svqz Stack; Stack = NULL; //Стек пуст. //Посетим первую непосещенную вершину графа и //поместим ее указатель на ее список смежности //в первоначально пустой стек. cout<<(*r).Key; (*r).Flag = FALSE; W_S (&Stack,(*r).Trail); while (Stack!=NULL) { //Рассмотрим "верхушку" стека. t = (*Stack).Element; if ((*(*t).Id).Trail!=NULL) { //У рассматриваемой вершины есть смежные. if ((*(*t).Id).Flag) //У рассматриваемой вершины есть // непосещенные смежные вершины. { //Посетим рассматриваемую вершину и поместим //указатель на ее список смежности в стек. cout<<(*(*t).Id).Key); (*(*t).Id).Flag = FALSE; W_S (&Stack,(*(*t).Id).Trail); } //У рассматриваемой вершины нет // непосещенных смежных вершин. else { t = (*Stack).Element; if ((*t).Next!=NULL) { //Заменяем верхушку стека // указателем на следующий элемент списка смежности. YDALENIE (&Stack,&t); W_S (&Stack,(*t).Next); } //Удаляем верхушку стека. else YDALENIE (&Stack,&t); } } //У рассматриваемой вершины нет смежных вершин. else { if ((*(*t).Id).Flag) { //Посетим рассматриваемую вершину. cout<<(*(*t).Id).Key; (*(*t).Id).Flag = FALSE; } t = (*Stack).Element; if ((*t).Next!=NULL) { //Заменяем верхушку стека указателем на //следующий элемент списка смежности. YDALENIE (&Stack,&t); W_S (&Stack,(*t).Next); } //Удаляем верхушку стека. else YDALENIE (&Stack,&t); } } }
Пример. Демонстрация рекурсивного и нерекурсивного обходов графа в глубину. Граф представлен структурой Вирта.
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; typedef struct L *Lref; // Тип: указатель на заголовочный узел. typedef struct T *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. Boolean Flag; //Флаг посещения узла при обходе. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. } Leader; //Описание типа дугового узла. typedef struct T { Lref Id; Tref Next; } Trailer; //Описание типа узла стека. typedef Tref TipElement; typedef struct Zveno *svqz; typedef struct Zveno { TipElement Element; //Указатель на список смежности. svqz Sled; } St; class Spisok { private: Lref Head; //Указатель на голову списка заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент // в конце списка заголовочных узлов. void SearchGraph (int, Lref *); void W_S (svqz *, TipElement); void YDALENIE (svqz *, TipElement *); public: Spisok() {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); } Lref GetHead() { return Head; } Lref GetTail() { return Tail; } void MakeGraph (); void PrintGraph (); void Depth_First_Search (Lref); void Depth_First_Search_1 (Lref); }; void main () { Spisok A; Lref t; //Рабочий указатель для перемещения // по списку заголовочных звеньев. //Построение графа и вывод его структуры Вирта. A.MakeGraph (); A.PrintGraph (); cout<<endl; //Рекурсивный обход графа в глубину. cout<<"Результат рекурсивного обхода...\n"; t = A.GetHead(); while (t!=A.GetTail()) { (*t).Flag = TRUE; t = (*t).Next; } A.Depth_First_Search (A.GetHead()); cout<<endl; //Нерекурсивный обход графа в глубину. cout<<"Результат нерекурсивного обхода...\n"; t = A.GetHead(); while (t!=A.GetTail()) { (*t).Flag = TRUE; t = (*t).Next;} A.Depth_First_Search_1 (A.GetHead()); cout<<endl; } void Spisok::SearchGraph (int w, Lref *h) //Функция возвращает указатель на заголовочный узел //с ключом w в графе, заданном структурой Вирта с указателем Head. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (Leader); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x, &p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<"("<<(*p).Key; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } } void Spisok::W_S (svqz *stk, TipElement el) //Помещение элемента el в стек stk. { svqz q=new (St); (*q).Element = el; (*q).Sled = *stk; *stk = q; } void Spisok::YDALENIE (svqz *stk, TipElement *klad) //Удаление звена из стека, заданного указателем *stk. //Значение информационного поля удаляемого звена сохраня- //ется в параметре klad. { svqz q; if (*stk==NULL) cout<<"Попытка выбора из пустого стека!\n"; else { *klad = (**stk).Element; q = *stk; *stk = (**stk).Sled; delete q; } } void Spisok::Depth_First_Search (Lref r) //Рекурсивный обход графа в глубину. r - указатель //на структуру Вирта. { Tref t; t = (*r).Trail; cout<<(*r).Key; (*r).Flag = FALSE; while (t!=NULL) { if ((*(*t).Id).Flag) Depth_First_Search ((*t).Id); t = (*t).Next; } } void Spisok::Depth_First_Search_1 (Lref r) //Нерекурсивный обход графа в глубину. //r - указатель на структуру Вирта. { Tref t; svqz Stack = NULL; //Стек пуст. //Посетим первую непосещенную вершину графа и //поместим ее указатель на ее список смежности //в первоначально пустой стек. cout<<(*r).Key; (*r).Flag = FALSE; W_S (&Stack,(*r).Trail); while (Stack!=NULL) { //Рассмотрим "верхушку" стека. t = (*Stack).Element; if ((*(*t).Id).Trail!=NULL) { //У рассматриваемой вершины есть смежные вершины. if ((*(*t).Id).Flag) //У рассматриваемой вершины есть // непосещенные смежные вершины. { //Посетим рассматриваемую вершину // и поместим указатель на ее список смежности в стек. cout<< (*(*t).Id).Key; (*(*t).Id).Flag = FALSE; W_S (&Stack,(*(*t).Id).Trail); } //У рассматриваемой вершины нет //непосещенных смежных вершин. else { t = (*Stack).Element; if ((*t).Next!=NULL) //Заменяем верхушку стека //указателем на следующий элемент списка смежности. { YDALENIE (&Stack,&t); W_S (&Stack,(*t).Next); } //Удаляем верхушку стека. else YDALENIE (&Stack,&t); } } //У рассматриваемой вершины нет смежных вершин. else { if ((*(*t).Id).Flag) //Посетим рассматриваемую вершину. { cout<<(*(*t).Id).Key; (*(*t).Id).Flag = FALSE; } t = (*Stack).Element; if ((*t).Next!=NULL) //Заменяем верхушку стека указателем на следующий // элемент списка смежности. { YDALENIE (&Stack,&t); W_S (&Stack,(*t).Next); } //Удаляем верхушку стека. else YDALENIE (&Stack,&t); } } }
Результат работы приложения приведен на рисунке 1:
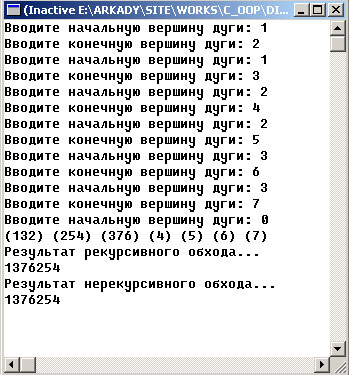
Рис.1. Результат работы приложения
Замечание [2, с.91]. Методика обхода в глубину очевидным образом переносится на ориентированные графы. Нетрудно проверить, что в случае ориентированного графа результатом вызова функций Depth_First_Search() и Depth_First_Search_1() будет посещение всех вершин u, таких что существует путь из v в u. В самом деле, при обходе в глубину ориентированного графа мы можем попасть в вершину y из вершины x только в том случае, если в графе есть дуга (x,y), т.е. мы должны двигаться вперед в направлении ориентации дуг, а возвращаться против ориентации (конечно же, в неориентированном графе таких ограничений нет)!
Функции языка LISP, реализующие алгоритм обхода графа в глубину, выглядят следующим образом [3, с.128].
Пример 2.
(DEFUN TESTDF (LAMBDA NIL
(PRINT "Построение графа.")
(SETQ GRAPH NIL) ;Инициализация
(PRINT "Введите список вершин графа:") (SETQ NODE (READ))
(PRINT "Введите список списков смежных вершин:")
(SETQ NODELIST (READ))
(PRINT (SETQ GRAPH (PAIRLIS NODE NODELIST GRAPH)))
(PRINT "Приступим к обходу графа в глубину...")
(PRINT "Введите вершину графа, с которой начнется обход:")
(SETQ ROOT (READ))
(DEPTHFIRST GRAPH ROOT)
))
; ------------------------------------
(DEFUN PAIRLIS (LAMBDA (KEY ADJ GRAPH)
; Построение графа из списка вершин KEY и списка списков
; смежных вершин ADJ путем добавления к существующему
; графу GRAPH
(COND ( (NULL KEY) GRAPH )
( (NULL ADJ) GRAPH )
( T (CONS (CONS (CAR KEY) (CAR ADJ))
(PAIRLIS (CDR KEY) (CDR ADJ) GRAPH)) )
)
))
; ------------------------------------
(DEFUN DEPTHFIRST (LAMBDA (GRAPH ROOT)
; Обход графа в глубину:
; GRAPH - граф, представленный структурой смежности в
; виде ассоциативного списка,
; ROOT - вершина, с которой начинается обход графа,
; Результат: список вершин графа в порядке посещения в глубину
(COND ( (NULL GRAPH) NIL )
( T (DEFI GRAPH (LIST ROOT) (LIST ROOT)) )
)
))
; --------------------------------------
(DEFUN DEFI (LAMBDA (GRAPH VISITED PATH)
; GRAPH - граф, представленный структурой смежности в
; виде ассоциативного списка,
; VISITED - список уже посещенных вершин,
; PATH - список вершин, определяющий путь посещения
(COND
( (NULL PATH) (REVERSE VISITED) )
( T (COND ( (NULL (EXPND GRAPH VISITED (CAR PATH)))
(DEFI GRAPH VISITED (CDR PATH)) )
( T (DEFI GRAPH
(CONS (EXPND GRAPH VISITED
(CAR PATH))
VISITED)
(CONS (EXPND GRAPH VISITED
(CAR PATH))
PATH)) )) )
)
))
; -----------------------------------------
(DEFUN EXPND (LAMBDA (GRAPH VISITED VERTEX)
; Выбор в графе GRAPH следующей еще не просмотренной
; вершины, смежной с вершиной VERTEX
(COND ( (NULL (NEIGHBOUR3 VERTEX GRAPH)) NIL )
( T (FIRSTNOTVISITED
VISITED
(NEIGHBOUR3 VERTEX GRAPH))
)
)
))
; --------------------------------------------
(DEFUN FIRSTNOTVISITED (LAMBDA (VISITED VLIST)
; Поиск первой непосещенной вершины в списке VLIST
; VISITED - список уже посещенных вершин
(COND ( (NULL VLIST) NIL )
( T (COND ( (NULL (MEMBER (CAR VLIST) VISITED))
(CAR VLIST)
)
( T (FIRSTNOTVISITED
VISITED
(CDR VLIST)) )) )
)
))
; ---------------------------------
(DEFUN NEIGHBOUR3 (LAMBDA (X GRAPH)
; Функция возвращает список вершин графа GRAPH, смежных с
; вершиной X
(COND ( (NULL (ASSOC X GRAPH)) NIL )
( T (CDR (ASSOC X GRAPH)) )
)
))
Тестовые примеры:
1) $ (TESTDF)
Построение графа.
Введите список вершин графа:
(1 2 3 4)
Введите список списков смежных вершин:
((2 3 4) (3 1) (4) ())
Приступим к обходу графа в глубину...
Введите вершину графа, с которой начнется обход:
2
(2 3 4 1)
2) $ (TESTBF)
Построение графа.
Введите список вершин графа:
(1 2 3 4 5 6 7)
Введите список списков смежных вершин:
((2 3) (4 5) (6 7) () () () ())
Приступим к обходу графа в глубину...
Введите вершину графа, с которой начнется обход:
1
(1 2 3 4 5 6 7)
Последний тестовый пример иллюстрируется следующим ориентированным графом:
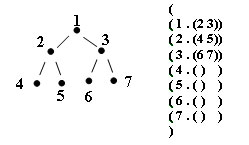
Рис.2. Пример графа
Программа работает следующим образом.
Если граф не пуст, то в два списка: VISITED - список уже посещенных вершин и PATH - список вершин, определяющих путь посещения, заносится первая вершина графа и после этого вызывается функция DEFI. Ее третий аргумент - список PATH - позволяет нам в любой момент вернуться к предыдущей вершине. Список VISITED используется для того, чтобы помнить о том, какие вершины уже посещались.
Выбор следующей вершины осуществляется с помощью функции EXPND. Именно работой этой функции определяется порядок обхода графа. В нашем случае, пока возможно, выбирается смежная вершина, т.е. на каждом шаге алгоритма делается попытка пройти "вглубь" графа. В противном случае из списка PATH удаляется первый элемент, и поиск возобновляется с предыдущей вершины.
Функция DEPTHFIRST возвращает список вершин графа в том порядке, в котором эти вершины посещались. Очевидно, что этот порядок зависит от вершины, с которой начинается просмотр.
Замечания.
- Алгоритмы поиска в глубину на графе изложены в монографиях [4, с.361-364], [2, с.88-91], [5, с.198-205], [6, с.323-327].
- Техника обхода в глубину использовалась в алгоритмах на графах долгое время, однако степень, с которой эта процедура позволяет раскрыть свойства графа, была обнаружена недавно.
Первой работой в этом направлении является статья Р.Е.Тарьяна, опубликованная в 1972 г. (ссылку см.в [4, с.426]). В этой работе представлена основная процедура поиска в глубину [4, с.364] и
алгоритмы отыскания двусвязных [4, с.371] и сильно связных компонент графа [4,c.375].
- M-нумерацией вершин графа называется нумерация вершин, соответствующая порядку их обхода при поиске в глубину [7,с.35].
(1) Касьянов В.H., Сабельфельд В.К. Сборник заданий по практикуму на ЭВМ. - М.: Наука, 1986. - 272 с.
(2) Липский В. Комбинаторика для программистов. - М.: Мир, 1988. - 213 с.
(3) Крюков А.П., Радионов А.Я., Таранов А.Ю., Шаблыгин Е.М. Программирование на языке R-Лисп. - М.: Радио и связь, 1991. - 192 с.
(4) Рейнгольд Э., Нивергельт Ю., Део H. Комбинаторные алгоритмы. Теория и практика. - М.: Мир, 1980. - 476 с.
(4) Пападимитриу Х., Стайнглиц К. Комбинаторная оптимизация. Алгоритмы и сложность. - М.: Мир, 1985. - 512 с.
(6) Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич - М.: Наука, 1990. - 384 с.
(7) Евстигнеев В.А. Применение теории графов в программировании. - М.: Наука, 1985. - 352 с.
На следующем шаге мы остановимся на алгоритме обхода графа в ширину.
