На этом шаге мы рассмотрим алгоритм обхода графов в ширину.
Перейдем теперь к другому алгоритму обхода графа, известному под названием обход в ширину (поиск в ширину). Прежде чем описать его, отметим, что при обходе в глубину чем позднее будет посещена вершина, тем раньше она будет использована. Это прямое следствие того факта, что просмотренные, но еще не использованные вершины накапливаются в стеке.
Обход графа в ширину, грубо говоря, основывается на замене стека очередью. После такой модификации чем раньше посещается вершина (помещается в очередь), тем раньше она используется (удаляется из очереди). Использование вершины происходит с помощью просмотра сразу всех еще непросмотренных вершин, смежных этой вершины. Таким образом, "поиск ведется как бы во всех возможных направлениях одновременно" [1, с.131]:
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; typedef struct Leader *Lref; // Тип: указатель на заголовочный узел. typedef struct Trailer *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct Leader { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. Boolean Flag; //Флаг посещения узла при обходе. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. }; //Описание типа дугового узла. typedef struct Trailer { Lref Id; Tref Next; }; //Описание типа узла очереди. typedef Lref TipElement; //Указатель на звено заголовочного списка. typedef struct Zveno *svqz; typedef struct Zveno { TipElement Element; //Указатель на список смежности. svqz Sled; }; class Spisok { private: Lref Head; //Указатель на голову списка заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент // в конце списка заголовочных узлов. void Udalenie_A (svqz *, svqz *, TipElement *); void Dobavlenie (svqz *, svqz *, TipElement); void SearchGraph (int, Lref *); public: Spisok() {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); } Lref GetHead() { return Head; } Lref GetTail() { return Tail; } void MakeGraph (); void PrintGraph (); void Breadth_First_Search (Lref); }; void main () { Spisok A; Lref t; //Рабочий указатель для перемещения // по списку заголовочных звеньев. //Построение графа и вывод его структуры Вирта. A.MakeGraph (); A.PrintGraph (); cout<<endl; //Нерекурсивный обход графа в ширину. cout<<"Результат нерекурсивного обхода...\n"; t = A.GetHead(); while (t!=A.GetTail()) { (*t).Flag = TRUE; t = (*t).Next; } A.Breadth_First_Search (A.GetHead()); cout<<endl; } void Spisok::SearchGraph (int w, Lref *h) //Функция возвращает указатель на заголовочный узел //с ключом w в графе, заданном структурой Вирта с указателем Head. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (Leader); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x, &p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<(*p).Key<<"("; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } } void Spisok::Dobavlenie (svqz *L, svqz *R, TipElement elem) //Добавление элемента elem в очередь, заданную указателями L и R. { svqz K = new (Zveno); K->Element = elem; K->Sled = NULL; if (*L==NULL) { (*L) = K; (*R) = K; } else { (*R)->Sled = K; (*R) = K; } } void Spisok::Udalenie_A (svqz *L, svqz *R, TipElement *A) //Удаление элемента из очереди, заданной указателями L и R и //помещение удаленного элемента в переменную A. { svqz q; if ((*L)!=NULL) if ((*L)->Sled!=NULL) { (*A) = (*L)->Element; q = (*L); (*L) = (*L)->Sled; delete q; } else { (*A) = (*L)->Element; delete *L; (*L) = (*R) = NULL; } } void Spisok::Breadth_First_Search (Lref H) //Обход графа в ширину, начиная с вершины, заданной указателем H //(нерекурсивный обход). { svqz L; //Указатель на начало очереди. svqz R; //Указатель на конец очереди. Lref p; //Рабочий указатель. Tref t; //Рабочий указатель. L = R = NULL; //Создание пустой очереди. Dobavlenie (&L,&R,H); H->Flag = FALSE; while ( L!=NULL ) //Пока очередь не пуста... { Udalenie_A (&L,&R,&p); cout << p->Key << " "; //Посещение вершины. t = p->Trail; while ( t!=NULL ) { if ( t->Id->Flag ) { Dobavlenie (&L,&R,t->Id); t->Id->Flag = FALSE; } t = t->Next; } } }
Результат работы приложения изображен на рисунке 1:
Рис.1. Результат работы приложения
Замечания.
- Как и в случае обхода графа в глубину, функцию Breadth_First_Search()
можно использовать без всяких модификаций и тогда, когда мы работаем с
ориентированным графом. Очевидно, что тогда посещаются только те вершины, до которых существует путь от вершины, с которой мы начинаем обход.
- Способ обхода дерева в ширину, называемый иногда обходом в гоpизонтальном поpядке, основан на посещении вершин деpева слева напpаво, уpовень за уpовнем вниз от коpня. Пpиведенный ниже нерекурсивный алгоpитм позволяет совершить обход деpева в шиpину, используя две очеpеди O1 и O2 [2, с.124-125]:
Взять пустые очеpеди O1 и O2. Поместить коpень в очеpедь O1. while (Одна из очеpедей O1 и O2 не пуста) if ( O1 не является пустой ) { Пусть p - узел, находящийся в голове очеpеди O1. Посетить веpшину p и удалить ее из O1. Поместить всех сыновей веpшины p в очеpедь O2, начиная со стаpшего сына. } else В качестве O1 взять непустую очеpедь O2, а в качестве O2 взять пустую очеpедь O1.
Перейдем к реализации алгоритма обхода графа в ширину на языке LISP [1, с.131].
(DEFUN TESTBF (LAMBDA NIL
(PRINT "Построение графа.")
(SETQ GRAPH NIL) ;Инициализация
(PRINT "Введите список вершин графа:") (SETQ NODE (READ))
(PRINT "Введите список списков смежных вершин:")
(SETQ NODELIST (READ))
(PRINT (SETQ GRAPH (PAIRLIS NODE NODELIST GRAPH)))
(PRINT "Приступим к обходу графа в ширину...")
(PRINT "Введите вершину графа, с которой начнется обход:")
(SETQ ROOT (READ))
(BREADTHFIRST GRAPH ROOT)
))
; ------------------------------------
(DEFUN PAIRLIS (LAMBDA (KEY ADJ GRAPH)
; Построение графа из списка вершин KEY и списка списков
; смежных вершин ADJ путем добавления к существующему
; графу GRAPH
(COND ( (NULL KEY) GRAPH )
( (NULL ADJ) GRAPH )
( T (CONS (CONS (CAR KEY) (CAR ADJ))
(PAIRLIS (CDR KEY) (CDR ADJ) GRAPH)) )
)
))
; --------------------------------------
(DEFUN BREADTHFIRST (LAMBDA (GRAPH ROOT)
; Обход графа GRAPH в ширину, начиная с вершины ROOT
; GRAPH - граф, представленный структурой смежности в
; виде ассоциативного списка,
; ROOT - вершина графа, с которой начинается обход,
; Результат: список вершин графа в порядке посещения
(BRFI
GRAPH
(LIST ROOT) ; Вершина ROOT уже просмотрена
(NEIGHBOUR3 ROOT GRAPH) ; Ожидают просмотра вершины, смежные
; вершине ROOT
)
))
; ---------------------------------------
(DEFUN BRFI (LAMBDA (GRAPH VISITED QUEUE)
; GRAPH - граф, представленный структурой смежности в
; виде ассоциативного списка,
; VISITED - список уже просмотренных вершин
; QUEUE - очередь вершин, ожидающих просмотра
(COND ( (NULL QUEUE) (REVERSE VISITED) )
( T (COND ( (MEMBER (CAR QUEUE) VISITED)
; Первая вершина в списке вершин, ожидающих
; просмотра уже посещалась
(BRFI GRAPH VISITED (CDR QUEUE)) )
( T (BRFI
GRAPH
; Вершина (CAR QUEUE) посещена
(CONS (CAR QUEUE) VISITED)
; В очередь вершин, ожидающих просмотра,
; помещаются вершины, смежные посещенной
(APPEND
QUEUE
(NEIGHBOUR3 (CAR QUEUE) GRAPH)))
)
)
)
)
))
; ---------------------------------
(DEFUN NEIGHBOUR3 (LAMBDA (X GRAPH)
; Функция возвращает список вершин графа GRAPH, смежных с
; вершиной X
(COND ( (NULL (ASSOC X GRAPH)) NIL )
( T (CDR (ASSOC X GRAPH)) )
)
))
Тестовые примеры:
1) $ (TESTBF)
Построение графа.
Введите список вершин графа:
(1 2 3 4 5)
Введите список списков смежных вершин:
((2 3 4) (1 3) (1 2 4) (1 3 5) (4))
Приступим к обходу графа в ширину...
Введите вершину графа, с которой начнется обход:
4
(4 1 3 5 2)
2) $ (TESTBF)
Построение графа.
Введите список вершин графа:
(1 2 3 4)
Введите список списков смежных вершин:
((2 3 4) (3) (4) ())
Приступим к обходу графа в ширину...
Введите вершину графа, с которой начнется обход:
2
(2 3 4)
3) $ (TESTBF)
Построение графа.
Введите список вершин графа:
(1 2 3 4 5 6 7)
Введите список списков смежных вершин:
((2 3) (4 5) (6 7) () () () ())
Приступим к обходу графа в ширину...
Введите вершину графа, с которой начнется обход:
1
(1 2 3 4 5 6 7)
Последний тестовый пример иллюстрируется следующим ориентированным графом:
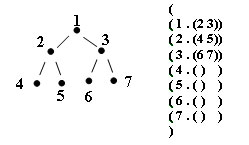
Рис.2. Пример графа
Мы видим, что при поиске в ширину смежные вершины последней просмотренной вершины добавляются в конец списка QUEUE функцией
(APPEND QUEUE (NEIGHBOUR3 (CAR QUEUE) GRAPH))),
в то время как новые вершины для просмотра берутся из начала этого списка, в который они помещаются функцией
(CONS (CAR QUEUE) VISITED),
т.е. содержимое параметр QUEUE используется как очередь в отличие от параметра PATH функции DEFI, содержимое которого "работает" как стек. Это приводит к тому, что в процессе работы функции BRFI просмотренные вершины в списке VISITED расположены в порядке невозрастания их расстояния от начальной вершины ROOT.
Замечания.
- Алгоритмы обхода графа в ширину изложены в монографиях [3, с.36-38], [4, с.92-94], [5, с.198-205], [6, с.238-242].
- Неформально под разметкой в монографии [7, с.28] понимается отображение, сопоставляющее пометки вершинам или дугам графа.
Метод разметки используется для построения алгоритмов распознавания различных свойств размеченных графов. Понятие пометки формализует при этом интересующее нас свойство графа или его частей. В качестве анализируемого размеченного графа часто выступает схема программы. Метод разметки использует тот факт, что свойства вершины графа определяются свойствами некоторых "соседей" этой вершины.
Для иллюстрации основной идеи алгоритмов разметки опишем алгоритм такого типа для решения одной очень простой задачи: определения достижимости вершин ориентированного графа от некоторой выделенной его вершины, называемой начальной.
Вершина v достижима от начальной, если существует путь, ведущий от начальной вершины к вершине v.
Множеством пометок здесь будет служить множество, составленное из двух значений, которые мы назовем "достижима" и "неизвестно" соответственно. Начальная разметка сопоставляет пометку "достижима" начальной вершине графа и "неизвестно" всем остальным вершинам. Дальнейший процесс построения необходимой разметки будет состоять в повторном применении правила разметки:
если некоторая вершина помечена пометкой "достижима"
то пометить пометкой "достижима" всех "наследников" этой вершины.
Процесс завершается, когда будет достигнута стационарная разметка, т.е. такая, которая не изменяется никаким применением правила разметки.
Отметим две особенности процесса разметки.
Во-первых, сразу же возникает вопрос о том, существует ли хотя бы одна стационарная разметка. Иначе говоря, может ли завершиться процесс разметки?
Другой вопрос связан с единственностью стационарной разметки. Дело в том, что процесс разметки описан как недетерминированный в том смысле, что на каждом его шаге имеется возможность выбирать, к какой из вершин применять правило разметки. Верно ли, что результирующая стационарная разметка (если она существует) не зависит от того, в каком порядке и к каким вершинам будет применяться правило разметки?
Естественно нас интересуют преимущественно такие процессы разметки, когда ответ на оба сформулированных выше вопроса положителен, т.е. когда стационарная разметка существует и единственна. Такие процессы называются алгоритмами разметки.
Ясно, что изученные нами алгоритмы обхода графа представляют собой простейшие алгоритмы разметки.
(1) Крюков А.П., Радионов А.Я., Таранов А.Ю., Шаблыгин Е.М. Программирование на языке R-Лисп. - М.: Радио и связь, 1991. - 192 с.
(2) Касьянов В.H., Сабельфельд В.К. Сборник заданий по практикуму на ЭВМ. - М.: Наука, 1986. - 272 с.
(3) Евстигнеев В.А. Применение теории графов в программировании. - М.: Наука, 1985. - 352 с.
(4) Липский В. Комбинаторика для программистов. - М.: Мир, 1988. - 213 с.
(5) Пападимитриу Х., Стайнглиц К. Комбинаторная оптимизация. Алгоритмы и сложность. - М.: Мир, 1985. - 512 с.
(6) Кук Д., Бейз Г. Компьютерная математика. - М.: Наука, 1990. - 384 с.
(7) Котов В.Е., Сабельфельд В.К. Теория схем программ. - М.: Наука, 1991. - 248 с.
На следующем шаге мы рассмотрим алгоритмы вычисления пути между фиксированными вершинами.
