На этом шаге мы рассмотрим алгоритм построения фундаментального множества циклов.
Тесно связана с задачей нахождения стягивающего дерева задача построения фундаментального множества циклов.
Если к стягивающему дереву (V,T) графа G=(V,E) мы добавим произвольное ребро e, принадлежащее E\T, то нетрудно отметить, что возникший при этом подграф (V, T в объединении с {e}) содержит в точности один цикл, который мы будем обозначать через Ce. Очевидно, что Ce содержит ребро e.
- Определение 1 [1, с.98].
- Множество J={Ce: e принадлежит E\T} будем называть фундаментальным множеством циклов графа G (относительно стягивающего дерева (V,T)).
Название "фундаментальный" связано с тем фактом, что каждый цикл графа G можно некоторым естественным способом получить из циклов множества J.
Введем для произвольных множеств A и B операцию A+B = (объединение A и B)\(пересечение A и B).
- Определение 2.
- Множество A+B будем называть симметрической разностью множеств A и B.
- Определение 3 [1, с.98].
- Множество C ребер графа называется псевдоциклом, если каждая вершина графа (V,C) имеет четную степень.
Примером псевдоцикла является пустое множество и произвольный цикл графа.
В монографии [1, c.99] доказана теорема о фундаментальном множестве циклов.
- Теорема.
- Пусть G=(V,E) - связный неориентированный граф, а (V,T) - его стягивающее дерево. Произвольный цикл графа
G можно однозначно представить как симметрическую разность некоторого числа фундаментальных
циклов. В общем случае произвольный псевдоцикл C графа G можно однозначно
представить в виде симметрической разности вида:
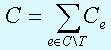
Реализуем теперь алгоритм, описанный в [1, с.100-101]. Этот алгоритм основывается на поиске в глубину и имеет структуру, аналогичную рекурсивному алгоритму нахождения стягивающего дерева. Каждая новая вершина, встречающаяся в процессе поиска, помещается в стек, представленный массивом Stack, и удаляется из стека после использования. Очевидно, что стек всегда содержит последовательность вершин с рассматриваемой в данный момент вершины v до корня. Поэтому если анализируемое нами ребро {v,u} замыкает цикл (WGN[v]>WGN[u]>0 и u не находится непосредственно под верхним элементом стека), то вершина u находится в стеке и цикл, замыкаемый ребром {v,u} представлен верхней группой элементов стека, начиная с v и кончая вершиной u.
Пример.
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; typedef struct Leader *Lref; // Тип: указатель на заголовочный узел. typedef struct Trailer *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct Leader { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. int WGN; //Характеристика узла. Tref Trail;//Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. }; //Описание типа дугового узла. typedef struct Trailer { Lref Id; Tref Next; }; class Spisok { private: Lref Head; //Указатель на голову списка заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент // в конце списка заголовочных узлов. Lref Stack[30]; //Рабочий стек. void SearchGraph (int, Lref *); void Cycle (Lref, int *, int *); public: Spisok() {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); } void MakeGraph (); void PrintGraph (); void Mn_Cycle(); }; void main () { Spisok A; //Построение графа и вывод его структуры Вирта. A.MakeGraph (); A.PrintGraph (); cout<<endl; //Построение множества фундаментальных циклов графа. A.Mn_Cycle(); } void Spisok::Mn_Cycle() //Построение множества фундаментальных циклов графа G. { cout << "Фундаментальные циклы:\n "; int num = 0, d = 0; //Количество элементов в стеке. Stack[0] = NULL; Lref t = Head; while ( t!=Tail ) { t->WGN = 0; t = t->Next; } t = Head; while ( t!=Tail ) { if ( t->WGN==0 ) Cycle(t,&d,&num); t = t->Next; } } void Spisok::Cycle (Lref r, int *d, int *num) //Нахождение фундаментального множества циклов для //компоненты связности, содержащей вершину r->Key. { Tref t; int i; (*d)++; Stack[(*d)] = r; (*num)++; r->WGN = *num; t = r->Trail; while ( t != NULL ) { if ( t->Id->WGN==0 ) Cycle (t->Id,d,num); else if (t->Id->Key != Stack[(*d)-1]->Key && r->WGN > t->Id->WGN) { i = *d; while ( Stack[i]->Key != t->Id->Key ) { cout << Stack[i]->Key << " "; i--; } cout << t->Id->Key << endl; } t = t->Next; } // Использованная вершина r->Key удаляется из стека. (*d)--; } void Spisok::SearchGraph (int w, Lref *h) //Функция возвращает указатель на заголовочный узел //с ключом w в графе, заданном структурой Вирта с указателем Head. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (Leader); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x, &p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<"("<<(*p).Key; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } }
Результат работы приложения изображен на рисунке 1:
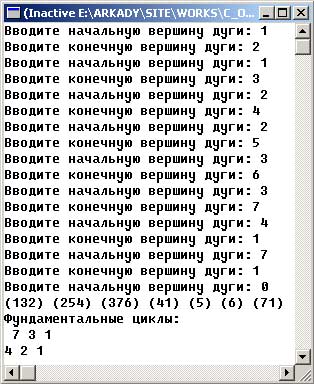
Рис.1. Результат работы приложения
Оценим теперь вычислительную сложность этого алгоритма [1, с.101].
Отметим сначала, что общее число шагов, как и во всех алгоритмах, основанных на поиске в глубину, имеет порядок O(m+n). К этому следует прибавить суммарную длину всех циклов. Эта длина не превосходит (m-n+1)n, что дает общую сложность алгоритма O(nm+n).
(1) Липский В. Комбинаторика для программистов: Пер. с польск. - М.: Мир, 1988. - 213 с.
Со следующего шага мы начнем знакомиться с алгоритмами с возвратом.
