На этом шаге мы рассмотрим алгоритм построения остова.
- Определение.
- Для произвольного связного неориентированного графа G=(V,E) каждое
дерево (V,T), где T - подмножество E, будем называть
стягивающим деревом (остовом, остовным деревом) графа G.
Ребра такого дерева будем называть ветвями,
а все остальные ребра графа будем называть хордами.
Максимальный подграф без циклов произвольного графа G называется стягивающим лесом графа G.
Задачу нахождения стягивающих деревьев можно понимать как поиск экономных путей, обеспечивающих связь между точками заданного множества без ненужного дублирования. Поэтому она применима во многих областях, например, при исследовании электрических цепей или при анализе схем программ.
Построение остова
Процедуры обхода графа в глубину и в ширину можно простым способом использовать для нахождения остовов. В обоих случаях достижение новой вершины графа u из вершины v вызывает "включение" в остовное дерево ребра {u,v}.
Сравните две процедуры:
void Spisok::Depth_First_Search (Lref r) //Рекурсивный обход графа в глубину. r - указатель //на структуру Вирта. { Tref t; t = (*r).Trail; cout<<(*r).Key; (*r).Flag = FALSE; while (t!=NULL) { if ((*(*t).Id).Flag) Depth_First_Search ((*t).Id); t = (*t).Next; } }
void Spisok::Ostov_Depth (Lref r) //Рекурсивный обход графа в глубину, соединенный с //нахождением ребра остовного дерева. //r - указатель на структуру Вирта. { Tref t; Lref s; s = r; t = (*r).Trail; (*r).Flag = FALSE; while ( t != NULL ) { if ((*(*t).Id).Flag) { cout << "(" << s->Key << "," << t->Id->Key << ") "; Ostov_Depth ((*t).Id); } t = (*t).Next; } }
Для доказательства того, что функция Ostov_Depth корректно строит остов связного графа, достаточно отметить следующие три факта [1, с.95]:
1) в момент выдачи на экран новой ветви {s->Key,t->Id->Key} оператором
cout << "(" << s->Key << "," << t->Id->Key << ") ";
в дереве уже существует путь из вершины Head->Key в s->Key, что легко доказывается по индукции. Таким образом, процедура строит связный граф;
2) каждая новая ветвь, добавляемая к множеству T (конечно, в процедуре множества нет: его роль играет экран дисплея!), соединяет уже рассмотренную вершину s->Key c новой вершиной t->Id->Key. Отсюда следует, что построенный граф не содержит циклов: действительно, последняя ветвь, "замыкающая" цикл, должна была бы соединить две уже рассмотренные вершины;
3) из свойства функции Depth_First_Search поиска в глубину следует, что функция Ostov_Depth просматривает все вершины связного графа.
Следовательно, граф (V,T), построенный процедурой Ostov_Depth, есть стягивающее дерево графа G.
Вычислительная сложность алгоритма есть, очевидно, O(n+m), т.е. того же порядка, что и поиск в глубину. Здесь: n - число вершин, а m - число ребер графа.
Приведем демонстрационный пример.
Пример 1. Нахождение стягивающего дерева связного графа, используя рекурсивный обход графа в глубину. Граф задан структурой Вирта.
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; typedef struct L *Lref; // Тип: указатель на заголовочный узел. typedef struct T *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. Boolean Flag; //Флаг посещения узла при обходе. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. } Leader; //Описание типа дугового узла. typedef struct T { Lref Id; Tref Next; } Trailer; //Описание типа узла стека. typedef Tref TipElement; typedef struct Zveno *svqz; typedef struct Zveno { TipElement Element; //Указатель на список смежности. svqz Sled; } St; class Spisok { private: Lref Head; //Указатель на голову списка заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент // в конце списка заголовочных узлов. void SearchGraph (int, Lref *); public: Spisok() {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); } Lref GetHead() { return Head; } Lref GetTail() { return Tail; } void MakeGraph (); void Ostov_Depth (Lref); void PrintGraph (); }; void main () { Spisok A; Lref t; //Рабочий указатель для перемещения // по списку заголовочных звеньев. //Построение графа и вывод его структуры Вирта. A.MakeGraph (); A.PrintGraph (); cout<<endl; //Построение стягивающего дерева (остова). cout<<"Остов: "; t = A.GetHead(); while (t!=A.GetTail()) { (*t).Flag = TRUE; t = (*t).Next; } A.Ostov_Depth (A.GetHead()); cout<<endl; } void Spisok::SearchGraph (int w, Lref *h) //Функция возвращает указатель на заголовочный узел //с ключом w в графе, заданном структурой Вирта с указателем Head. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (Leader); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x, &p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while (( r != NULL )&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<"("<<(*p).Key; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } } void Spisok::Ostov_Depth (Lref r) //Рекурсивный обход графа в глубину, соединенный с //нахождением ребра остовного дерева. //r - указатель на структуру Вирта. { Tref t; Lref s; s = r; t = (*r).Trail; (*r).Flag = FALSE; while ( t != NULL ) { if ((*(*t).Id).Flag) { cout << "(" << s->Key << "," << t->Id->Key << ") "; Ostov_Depth ((*t).Id); } t = (*t).Next; } }
Результат работы приложения изображен на рисунке 1:
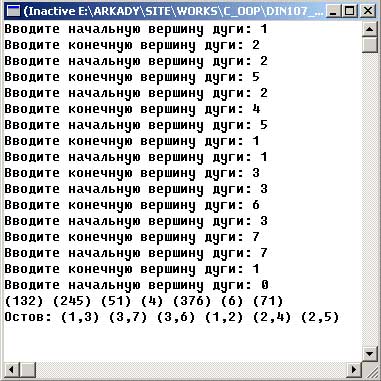
Рис.1. Результат работы приложения
Ясно, что далеко не всякий ориентированный граф имеет остов. Например, граф, заданный следующим списком дуг: (1,2), (1,6), (1,7), (6,7), (7,2), (5,7), (2,5), (3,2), (3,5) остова не имеет.
Подобным же способом можно построить остов, используя обход графа в ширину. В функции Ostov_Breadth используются две очереди.
Пример 2. Нахождение стягивающего дерева связного графа с использованием нерекурсивного обхода графа в ширину. Граф задан структурой Вирта.
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; typedef struct Leader *Lref; // Тип: указатель на заголовочный узел. typedef struct Trailer *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct Leader { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. Boolean Flag; //Флаг посещения узла при обходе. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. }; //Описание типа дугового узла. typedef struct Trailer { Lref Id; Tref Next; }; //Описание типа узла очереди. typedef Tref TipElement; //Указатель на звено заголовочного списка. typedef struct Zveno *svqz; typedef struct Zveno { TipElement Element; //Указатель на список смежности. svqz Sled; }; //Описание типа узла очереди указателей на //узлы списков смежности. typedef Lref TipElement1; typedef struct Zveno1 *svqz1; typedef struct Zveno1 { TipElement1 Element; //Указатель на заголовочный узел. svqz1 Sled; }; class Spisok { private: Lref Head; //Указатель на голову списка заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент // в конце списка заголовочных узлов. void Udalenie_A (svqz *, svqz *, TipElement *); void Udalenie_A1 (svqz1 *, svqz1 *, Lref *); void Dobavlenie (svqz *, svqz *, TipElement); void Dobavlenie1 (svqz1 *, svqz1 *, Lref); void SearchGraph (int, Lref *); public: Spisok() {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); } Lref GetHead() { return Head; } Lref GetTail() { return Tail; } void MakeGraph (); void PrintGraph (); void Ostov_Breadth (); }; void main () { Spisok A; Lref t; //Рабочий указатель для перемещения //по списку заголовочных звеньев. //Построение графа и вывод его структуры Вирта. A.MakeGraph (); A.PrintGraph (); cout<<endl; //Построение стягивающего дерева (остова). cout<<"Остов: "; t = A.GetHead(); while (t!=A.GetTail()) { (*t).Flag = TRUE; t = (*t).Next; } A.Ostov_Breadth (); cout<<endl; } void Spisok::SearchGraph (int w, Lref *h) //Функция возвращает указатель на заголовочный узел //с ключом w в графе, заданном структурой Вирта с указателем Head. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (Leader); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x, &p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<(*p).Key<<"("; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } } void Spisok::Dobavlenie (svqz *L, svqz *R, TipElement elem) //Добавление элемента elem в очередь, заданную указателями L и R. { svqz K = new (Zveno); K->Element = elem; K->Sled = NULL; if (*L==NULL) { (*L) = K; (*R) = K; } else { (*R)->Sled = K; (*R) = K; } } void Spisok::Dobavlenie1 (svqz1 *L, svqz1 *R, Lref elem) //Добавление элемента elem в очередь, заданную указателями L и R. { svqz1 K = new (Zveno1); K->Element = elem; K->Sled = NULL; if (*L==NULL) { (*L) = K; (*R) = K; } else { (*R)->Sled = K; (*R) = K; } } void Spisok::Udalenie_A (svqz *L, svqz *R, TipElement *A) //Удаление элемента из очереди, заданной указателями L и R и //помещение удаленного элемента в переменную A. { svqz q; if ((*L)!=NULL) if ((*L)->Sled!=NULL) { (*A) = (*L)->Element; q = (*L); (*L) = (*L)->Sled; delete q; } else { (*A) = (*L)->Element; delete *L; (*L) = (*R) = NULL; } } void Spisok::Udalenie_A1 (svqz1 *L, svqz1 *R, Lref *A) //Удаление элемента из очереди, заданной указателями L и R и //помещение удаленного элемента в переменную A. { svqz1 q; if ((*L)!=NULL) if ((*L)->Sled!=NULL) { (*A) = (*L)->Element; q = (*L); (*L) = (*L)->Sled; delete q; } else { (*A) = (*L)->Element; delete *L; (*L) = (*R) = NULL; } } void Spisok::Ostov_Breadth () //Обход графа, заданного указателем r в ширину (нерекурсивный //обход), соединенный с построением стягивающего дерева. { svqz L; //Указатель на начало очереди. svqz R; //Указатель на конец очереди. svqz1 L1; //Указатель на начало очереди заглавных узлов. svqz1 R1; //Указатель на конец очереди заглавных узлов. Tref s; //Рабочий указатель. Tref t; //Рабочий указатель. Tref Tail1;//Указатель на фиктивный элемент в очереди L,R; Lref v; //Рабочий указатель. Tail1 = new (Trailer); //Построили фиктивный элемент. //Создали пустые очеpеди. L = R = NULL; L1 = R1 = NULL; //Посетим первую непосещенную вершину графа. Head->Flag = FALSE; t = Head->Trail; while ( t != NULL ) { Dobavlenie (&L,&R,t); t = t->Next; } Dobavlenie (&L,&R,Tail1); v = Head; while ( L!=NULL ) //Пока очередь не пуста... { Udalenie_A (&L,&R,&t); if ( t != Tail1 ) { if (t->Id->Flag) { cout << "(" << v->Key << "," << t->Id->Key << ") "; t->Id->Flag = FALSE; } s = t->Id->Trail; Dobavlenie1 (&L1,&R1,t->Id); while (s != NULL ) { if (s->Id->Flag) { Dobavlenie (&L,&R,s); t->Id->Flag = FALSE; } s = s->Next; } Dobavlenie (&L,&R,Tail1); } else Udalenie_A1 (&L1,&R1,&v); } }
Результат работы приложения изображен на рисунке 2:
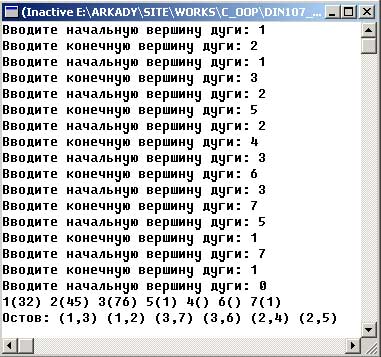
Рис.2. Результат работы приложения
Замечание. Приведенные программы легко модифицируются для произвольных графов, не обязательно связных.
Обратимся теперь к реализации алгоритма построения остовного дерева связного графа на языке LISP. Для этого вспомним, что при поиске в глубину новая вершина добавляется к списку уже пройденных вершин только в том случае, когда она в этом списке отсутствует. Поэтому последовательность вершин, соответствующая удлинению списка PATH при работе функции DEFI, представляет собой простой0(т.е. без самопересечений) путьв просматриваемом графе.
После этих замечаний можно написать функцию, значением которой является список ребер, представляющий остовное дерево графа:
Программа 1 [2, с.130-131].
(DEFUN SPANDF (LAMBDA (GRAPH ROOT) ; Построение остовного дерева графа GRAPH с корнем ROOT: ; GRAPH - граф, представленный структурой смежности в ; виде ассоциативного списка, ; ROOT - корень остовного дерева, ; Результат: список ребер остовного дерева, полученного ; с помощью поиска в глубину (COND ( (NULL GRAPH) NIL ) ( T (SPDF GRAPH (LIST ROOT) (LIST ROOT)) ) ) )) ; -------------------------------------- (DEFUN SPDF (LAMBDA (GRAPH VISITED PATH) ; GRAPH - граф, представленный структурой смежности в ; виде ассоциативного списка, ; VISITED - список уже посещенных вершин, ; PATH - список вершин, определяющий путь посещения (COND ( (NULL PATH) NIL ) ( T (COND ( (NULL (EXPND GRAPH VISITED (CAR PATH))) (SPDF GRAPH VISITED (CDR PATH)) ) ( T (CONS (CONS (CAR PATH) (EXPND GRAPH VISITED (CAR PATH))) (SPDF GRAPH (CONS (EXPND GRAPH VISITED (CAR PATH)) VISITED) (CONS (EXPND GRAPH VISITED (CAR PATH)) PATH))) )) ) ) )) ; ----------------------------------------- (DEFUN EXPND (LAMBDA (GRAPH VISITED VERTEX) ; Выбор в графе GRAPH следующей еще не просмотренной ; вершины, смежной с вершиной VERTEX (COND ( (NULL (NEIGHBOUR3 VERTEX GRAPH)) NIL ) ( T (FIRSTNOTVISITED VISITED (NEIGHBOUR3 VERTEX GRAPH)) )) )) ; -------------------------------------------- (DEFUN FIRSTNOTVISITED (LAMBDA (VISITED VLIST) ; Поиск первой непосещенной вершины в списке VLIST ; VISITED - список уже посещенных вершин (COND ( (NULL VLIST) NIL ) ( T (COND ( (NULL (MEMBER (CAR VLIST) VISITED)) (CAR VLIST) ) ( T (FIRSTNOTVISITED VISITED (CDR VLIST)) )) )) )) ; --------------------------------- (DEFUN NEIGHBOUR3 (LAMBDA (X GRAPH) ; Функция возвращает список вершин графа GRAPH, смежных с ; вершиной X (COND ( (NULL (ASSOC X GRAPH)) NIL ) ( T (CDR (ASSOC X GRAPH)) )) ))
Тестовые примеры:
1) $ (SPANDF '((1 . (2 3)) (2 . (4 5)) (3 . (6 7))) 1)
((1 . 2) (2 . 4) (2 . 5) (1 . 3) (3 . 6) (3 . 7))
2) $ (SETQ A1 '((1 . (2 4)) (2 . (1 3 5)) (3 . (2 4 6))
(4 . (1 3 6 7)) (5 . (2 6 8 9)))
((1 2 4) (2 1 3 5) (3 2 4 6) (4 1 3 6 7) (5 2 6 8 9))
$ (SETQ A2 '((6 . (3 4 5 7 9)) (7 . (4 6)) (8 . (5)) (9 . (5 6)))
((6 3 4 5 7 9) (7 4 6) (8 5) (9 5 6))
$ (SPANDF (APPEND A1 A2) 1)
((1 . 2) (2 . 3) (3 . 4) (4 . 6) (6 . 5) (5 . 8) (5 . 9) (6 . 7))
Теперь мы зададимся вопросом, какими свойствами будет обладать остовное дерево, построенное с помощью процедуры обхода графа в ширину? Мы уже упоминали о том, что при обходе в ширину просмотренные вершины располагаются в порядке неубывания их расстояния от начальной вершины. Поэтому в остовном дереве, построенном с помощью обхода в ширину, единственный путь, соединяющий какую-либо вершину с начальной, совпадает с кратчайшим путем в исходном графе между этими двумя вершинами.
Необходимые для построения остовного дерева с помощью обхода в ширину изменения в функции BRFI более существенны по сравнению с аналогичными изменениями в функции DEFI. Дело в том, что при поиске в ширину нам не нужна была информация о предшественнике рассматриваемой вершины - в этом смысле поиск в ширину нелокален. Поэтому вместо очереди вершин, предназначенных для просмотра, мы введем очередь, состоящую непосредственно из элементов структуры смежности.
Программа 2 [3, с.132-133].
(DEFUN SPANBF (LAMBDA (GRAPH ROOT) ; Построение остовного дерева графа GRAPH с корнем ; в вершине ROOT при помощи обхода графа в ширину: ; GRAPH - граф, представленный структурой смежности в ; виде ассоциативного списка, ; ROOT - корень остовного дерева (SPBF GRAPH (LIST ROOT) (CDR (ASSOC ROOT GRAPH)) NIL (CAR (ASSOC ROOT GRAPH))) )) ; --------------------------------------------------- (DEFUN SPBF (LAMBDA (GRAPH VISITED HEAD QUEUE FATHER) ; GRAPH - граф, представленный структурой смежности в ; виде ассоциативного списка, ; VISITED - список уже посещенных вершин, ; HEAD - список вершин для просмотра, ; QUEUE - очередь списка вершин для просмотра, ; FATHER - предок просматриваемых вершин (COND ( (NULL HEAD) (COND ( (NULL QUEUE) NIL ) ( T (SPBF GRAPH VISITED (CDAR QUEUE) (CDR QUEUE) (CAAR QUEUE)) )) ) ( T (COND ( (MEMBER (CAR HEAD) VISITED) (SPBF GRAPH VISITED (CDR HEAD) QUEUE FATHER) ) ( T (CONS (CONS FATHER (CAR HEAD)) (SPBF GRAPH (CONS (CAR HEAD) VISITED) (CDR HEAD) (APPEND QUEUE (LIST (ASSOC (CAR HEAD) GRAPH))) FATHER)) )) ) ) ))
Тестовые примеры:
1) $ (SPANBF '((1 . (2 4)) (2 . (1 3)) (4 . (1 3)) (3 . (1 4))) 1)
((1 . 2) (1 . 4) (2 . 3))
$ (SPANBF '((1 . (2 4)) (2 . (1 3)) (4 . (1 3)) (3 . (1 4))) 2)
((2 . 1) (2 . 3) (1 . 4))
$ (SPANBF '((1 . (2 4)) (2 . (1 3)) (4 . (1 3)) (3 . (1 4))) 3)
((3 . 1) (3 . 4) (1 . 2))
$ (SPANBF '((1 . (2 4)) (2 . (1 3)) (4 . (1 3)) (3 . (1 4))) 4)
((4 . 1) (4 . 3) (1 . 2))
2) $ (SPANBF '((1 . (2 3)) (2 . (4 5)) (3 . (6 7))) 1)
((1 . 2) (1 . 3) (2 . 4) (2 . 5) (3 . 6) (3 . 7))
3) $ (SETQ A1 '((1 . (2 4)) (2 . (1 3 5)) (3 . (2 4 6))
(4 . (1 3 6 7)) (5 . (2 6 8 9)))
((1 2 4) (2 1 3 5) (3 2 4 6) (4 1 3 6 7) (5 2 6 8 9))
$ (SETQ A2 '((6 . (3 4 5 7 9)) (7 . (4 6)) (8 . (5)) (9 . (5 6)))
((6 3 4 5 7 9) (7 4 6) (8 5) (9 5 6))
$ (SPANBF (APPEND A1 A2) 1)
((1 . 2) (1 . 4) (2 . 3) (2 . 5) (4 . 6) (4 . 7) (5 . 8) (5 . 9))
Обратите внимание, что при работе функции SPBF параметр HEAD всегда есть список соседей вершины, определяемой параметром FATHER, что позволяет знать предшественника текущей вершины.
(1) Липский В. Комбинаторика для программистов. - М.: Мир, 1988. - 213 с.
(2) Turbo Pascal Version 3.0 Reference Manual. Borland International, 1985.
(3) Крюков А.П., Радионов А.Я., Таранов А.Ю., Шаблыгин Е.М. Программирование на языке R-Лисп. - М.: Радио и связь, 1991. - 192 с.
На следующем шаге мы рассмотрим алгоритм построения остова наименьшей стоимости.
