На этом шаге мы рассмотрим понятие числа независимости графа и алгоритм нахождения наибольшего независимого множества.
- Определение 1 [1, с.44].
- Рассмотрим неориентированный граф G=(V,E).
Независимое множество вершин (известное также как внутренне устойчивое множество) есть множество вершин графа G, такое, что любые две вершины в нем не смежны (никакая пара вершин не соединена ребром).
Независимое множество называется максимальным, когда нет другого независимого множества, в которое оно бы входило.
Например, рассмотрим граф:
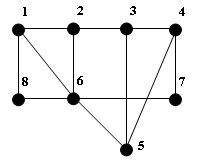
Рис.1. Пример графа
Для данного графа множества вершин
- {7,8,2}, {1,3}, {7,8,2,5} - независимые;
- {1,3,7}, {4,6}, {7,8,2,5} - максимальные.
Следовательно, в рассмотренном графе больше одного независимого множества.
- Определение 2 [1, с.45]
- Если Q является семейством всех независимых множеств графа G, то число
a(G) = max |S| S принадлежит Qназывается числом независимости графа G, а множество S*, на котором этот максимум достигается, называется наибольшим независимым множеством.
Например, для изображенного выше графа семейство максимальных независимых множеств таково: {8,7,2,5}, {1,3,7}, {2,4,8}, {6,4}, {6,3}, {1,4}, {7,5,1}, {3,7,8}.
Наибольшее из этих множеств имеет 4 элемента и, следовательно, a(G)=4.
Множество {8,7,2,5} является наибольшим независимым множеством.
Ясно, что понятие, противоположное максимальному независимому множеству, есть максимальный полный подграф (клика).
Совершенно очевидно, что максимальное независимое множество графа G соответствует клике графа G~ и наоборот, где G~ - дополнение графа G.
Это утверждение лежит в основе работы алгоритма, реализованного ниже на языке C++.
Пример.
//Нахождение всех независимых множеств в графе, заданном //структурой Вирта, с использованием клики. #include <iostream.h> #define TRUE 1 #define FALSE 0 #define Node 20 //Максимальное количество вершин в графе. typedef int Boolean; typedef struct L *Lref; // Тип: указатель на заголовочный узел. typedef struct T *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. Boolean Flag; //Флаг посещения узла при обходе. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. }; //Описание типа дугового узла. typedef struct T { Lref Id; Tref Next; }; class Spisok { private: Lref Head; //Указатель на голову списка заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент // в конце списка заголовочных узлов. int X[20]; //Результат работы программы. void SearchGraph (int, Lref *); Lref Search(int); public: Spisok() {//Инициализация списка заголовочных узлов. Head = Tail = new (L); } Lref GetHead() { return Head; } Lref GetTail() { return Tail; } void MakeGraph (); void PrintGraph (); void AddGraph(int, int); void DeleteGraph(int, int); void Clique (int, int); void X1 (Lref t) {X[1] = t->Key;}; }; void main () { Spisok A; Lref t; //Рабочий указатель для перемещения // по списку заголовочных звеньев. Lref t1; int n=0; //Построение графа и вывод его структуры Вирта. A.MakeGraph (); A.PrintGraph (); cout<<endl; //Инициализация и подсчет количества вершин графа. t = A.GetHead(); while (t!=A.GetTail()) { n++; t = (*t).Next; } // ------------------------------------ //Нахождение всех клик в графе Head. for (int i=3;i<=n;i++) { //i - количество вершин в клике (i<=3). cout << "Перечислим все клики длины " << i << endl; t = A.GetHead(); while (t!=A.GetTail()) { //Инициализация. t1 = A.GetHead(); while (t1!=A.GetTail()) { t1->Flag = TRUE; t1 = t1->Next; } A.X1(t); t->Flag = FALSE; //Отыскание клики с i вершинами, "начинающейся" в вершине t. A.Clique (2,i); t = t->Next; } } } Lref Spisok::Search (int w) //Функция возвращает указатель на заголовочный узел //ключом w. Если узел отсутствует, то функция возвращает NULL . { Lref h = Head; (*Tail).Key = w; //Поиск "с барьером". while ((*h).Key!=w) h = (*h).Next; if (h==Tail) //В списке заголовочных узлов нет узла с ключом w. h = NULL; return h; } void Spisok::AddGraph (int x,int y) //Добавление дуги (x,y) (если ее не было!) к структуре //Вирта, соответствующей ориентированному графу Head. { Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия в графе данной дуги. //Определим, существует ли в графе дуга (x,y)? SearchGraph (x,&p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) { //Если дуга отсутствует, то поместим её в граф. t = new (T); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } } void Spisok::DeleteGraph (int x,int y) //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу //и полученную удалением дуги (x,y). { Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия в графе данной дуги. //Определим, существует ли в графе дуга (x,y)? p=Search (x); q= Search (y); if ((p!=NULL)&&(q!=NULL)) { //Вершины x и y в графе есть. r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (Res) //Если дуга существует, то удалим её. if (r==(*p).Trail) { (*p).Trail = (*(*p).Trail).Next; delete r; (*q).Count--; } else { t = (*p).Trail; while ((*t).Next!=r) t = (*t).Next; (*t).Next = (*(*t).Next).Next; delete r; (*q).Count--; } } } void Spisok::SearchGraph (int w, Lref *h) //Функция возвращает указатель на заголовочный узел //с ключом w в графе, заданном структурой Вирта с указателем Head. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (L); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x, &p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (T); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<< (*p).Key << "("; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } } void Spisok::Clique (int k, int m) //Нахождение всех клик, содержащих m вершин, в графе, //заданном структурой Вирта с указателем Head, //k - количество вершин в частичном решении. { Tref r,r1; //Рабочие указатели. Lref p,q; //Рабочие указатели. Lref t; //Указатель на k-ю вершину частичного решения. int v; //Вершина - кандидат на дополнение к частичному решению. Boolean Res; //Флаг клики. Boolean Res1;//Флаг существования ребра. int i; //Параметр цикла. SearchGraph (X[k-1], &t); r = t->Trail; while ( r != NULL ) { v = r->Id->Key; //Проверим, смежна ли вершина v с вершинами X[1],X[2],...,X[k-1]. Res = TRUE; for (i=1;i<=k-1;i++) { //Cуществует ли в графе ребро (X[i],v)? SearchGraph (v, &p); SearchGraph (X[i], &q); r1 = p->Trail; Res1 = FALSE; while (r1 != NULL && !Res1) if ( r1->Id==q ) Res1 = TRUE; else r1 = r1->Next; Res = (Res && Res1); } if (!Res) r->Id->Flag = FALSE; // -------------------------- if (k==m && Res) //Количество вершин в графе равно m, и //вершины X[1],X[2],...,X[k] образуют клику. { //Вывод клики на экран дисплея. for (i=1;i<=k-1;i++) cout << X[i] << " "; cout << v << endl; } else if ( r->Id->Flag ) { X[k] = r->Id->Key; r->Id->Flag = FALSE; Clique (k+1,m); r->Id->Flag = TRUE; } r = r->Next; } }
Замечания.
- Пусть нам необходимо отыскать "специальное" множество M ребер графа G
такое, что в M не должно быть смежных ребер. Множество M называют
паросочетанием, а множество M* - с наибольшей мощностью - является
наибольшим паросочетанием, его можно называть также наибольшим независимым множеством ребер [1, с.66].
Связь между наибольшими независимыми множествами вершин и наибольшими паросочетаниями устанавливается с помощью реберных графов.
- [2, с.73]. Одна из чисто житейских интерпретаций понятия независимости состоит в
следующем. Определенный человек желает устроить юбилей с максимальным
числом гостей из своих знакомых. Стремясь сделать юбилейный вечер приятным, он должен организовать все так, чтобы на этом вечере присутствовали
люди, симпатизирующие друг другу. Так как отношение "симпатии" не является транзитивным, то ему для достижения цели придется находить число
независимости графа своих знакомых.
Этот граф устроен следующим образом. Вершины его - знакомые юбиляра. Две вершины смежны, если соответствующие знакомые друг другу не симпатизируют. Нетрудно понять, что число независимости этого графа и представляет тот самый максимальный контингент приглашенных, который может себе позволить юбиляр.
- Рассмотрим следующую шахматную задачу. Сколько ферзей можно установить на шахматной жоске, чтобы они не "били" друг друга?
Нетрудно убедиться, что искомое число равно 8, что соответствует утверждению о числе
независимости графа шахматной доски G.
Ясно, что аналогичные задачи могут быть сформулированы и для других шахматных фигур.
- [2, с.74]. Пусть Gn - граф "делимости" натуральных чисел. Вершины Gn - это числа
1,2,...,n, и две вершины i, j смежны только в том случае, когда их наибольший общий делитель больше единицы. На рисунке изображен граф G8:
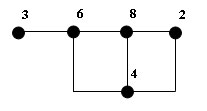
Нетрудно показать, что справедливо следущее равенство:
a(Gn)=p(n),
где функция p(n) - число простых чисел, не превосходящих n. Полученное соотношение показывает, что нахождение числа независимости в общем случае не является простой задачей, уже хотя бы потому, что для частного вида графа она эквивалентна традиционно трудной задаче вычисления значения функции p(n).
[2(log2n-log2log2n)]<=a(G)<=[2(log2n-log2log2n)]+3
(1) Кристофидес Н. Теория графов. Алгоритмический подход. - М.: Мир, 1978. - 432 с.
(2) Компьютер и задачи выбора. - М.: Наука, 1989. - 208 с.
(3) Коршунов А.Д. Основные свойства случайных графов с большим числом вершин и ребер // УМН, 1985, т.40, вып.1 (241), с.107-173.
Со следующего шага мы начнем знакомиться с раскрасками.
