На этом шаге мы приведем общие сведения о раскрасках.

    Разнообразные задачи, возникающие при планировании производства, составлении графиков осмотра, хранении и транспортировке товаров и т.д. могут быть представлены часто как задачи теории графов, тесно связанные с так называемой "задачей раскраски".

    Пусть рассматриваемые графы являются неориентированными и не имеют петель.

Определение [1, с.73].

Граф G называют r-хроматическим, если его вершины могут быть раскрашены с использованием r цветов (красок) так, что не найдется двух смежных вершин одного цвета.

    Наименьшее число r, такое, что граф G является r-хроматическим, называется хроматическим числом графа G и обозначается g(G).

    Например, полный n-вершинный граф G имеет хроматическое число, равное n, а всякое дерево имеет хроматическое число равное двум.

    Задача нахождения хроматического числа графа называется задачей о раскраске (задачей раскраски) графа.

    Соответствующая хроматическому числу раскраска вершин разбивает множество вершин графа на r подмножеств, каждое из которых содержит вершины одного цвета. Эти множества являются независимыми, поскольку в пределах одного множества нет двух смежных вершин.

    Вообще говоря, хроматическое число графа нельзя найти, зная только число вершин и число ребер графа. При известных величинах n (число вершин), m (число ребер) и d₁, d₂, ..., d_n (степени вершин графа) можно получить верхнюю и нижнюю оценки для хроматического числа графа.

    Вначале отметим, что поскольку между кликами графа G и максимальными независимыми множествами дополнительного графа G~ существует взаимно однозначное соответствие, то справедливы равенства

    r(G)= a(G~) и r(G~0)=a(G),

    Теперь, поскольку по крайней мере r(G) цветов требуется для раскраски соответствующей клики графа G (той самой клики, которая "определяет" кликовое число графа G), что r(G) является нижней оценкой хроматического числа, т.е. g(G)>=r(G).

    У.Татт в 1954 г. показал, что можно построить граф G с кликовым числом равным 2, который будет иметь произвольно большое заданное значение хроматического числа (граф Татта).

    Поскольку a(G) равно мощности наибольшего множества попарно несмежных вершин графа G, то оно совпадает также с мощностью наибольшего множества вершин в G, которые могут быть окрашены в один цвет, и, следовательно,

    g(G) >= [n/a(G)]

    Нижние оценки хроматического числа безусловно более интересны, чем верхние, поскольку (если они достаточно близки к истинному значению) они могут быть использованы в процедуре вычисления g(G), включающей дерево поиска. В то же время верхние оценки хроматического числа подобного применения не находят.

    Тем не менее в литературе приводятся формулы для вычисления верхних оценок хроматического числа; так Р.Бруксом предложена следующая легко вычисляемая оценка:

    g(G) <= 1 + max [d(vi)+1]
                vi принадлежит V

    Приведем важную для построения алгоритма раскраски теорему.

Теорема [1, с.80].

Если граф является r-хроматическим, то он может быть раскрашен с использованием r (или меньшего числа) красок с помощью следующей процедуры: сначала в один цвет окрашивается некоторое максимальное независимое множество S₁[G], затем окрашивается в следующий цвет множество S₁[X-S₁[G]] и т.д. до тех пор, пока не будут раскрашены все вершины.

    Раскраску указанного в теореме вида будем называть оптимальной независимой раскраской.

    Приведенный ниже пример показывает шаги алгоритма, описанного в теореме.

    Максимальным независимым множеством вершин для графа

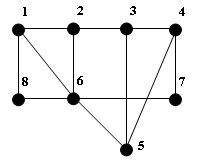
Рис.1. Пример графа

является {8,7,2,5}. Удаляем данные вершины из графа, предварительно присвоив им цвет 1:

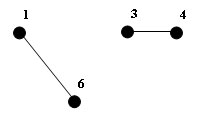
Рис.2. Результат удаления

    Максимальными независимыми множествами вершин для полученного графа будут {1,3}, {1,4}, {6,3}, {6,4}. Удалим из графа, например, вершины 1 и 4, присвоив им цвет 2. Оставшиеся в графе вершины 3 и 6 получают цвет 3.

    Изобразим результат раскраски:

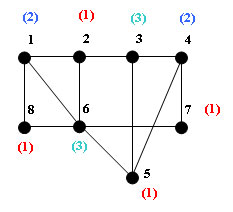
Рис.3. Результат раскраски

    На следующем шаге мы рассмотрим алгоритмы раскраски.

Предыдущий шаг Содержание Следующий шаг