На этом шаге мы рассмотрим алгоритмы, определяющие изоморфизм графов.
Напомним сначала Вам несколько определений.
- Определение 1.
-
Пусть G и H - графы, f - взаимно однозначное отображение множества
V(G) на множество V(H) и g - взаимно однозначное отображение E(G) на
E(H). Обозначим Q упорядоченную пару (f,g). Будем говорить, что Q есть
изоморфное отображение (изоморфизм) графа G на граф H, если выполняется
следующее условие: вершина x инцидентна ребру A в графе G тогда и
только тогда, когда вершина fx инцидентна ребру gA в графе H.
Если такой изоморфизм Q существует, то будем говорить, что графы G и H изоморфны. Ясно, что в этом случае
|V(G)| = |V(H)| и |E(G)| = |E(H)|.Мы можем рассматривать Q как операцию, преобразующую граф G в граф H, и в соответствии с этим писать QG=H. Удобно также писать Qv=fv и QA=gA (для каждой вершины v и каждого ребра A графа G).
Автоморфизмом графа G называется изоморфизм графа G на себя.
Всякий граф G имеет тождественный (или тривиальный) автоморфизм I, такой, что Ix=x для каждого ребра x и каждой вершины x из G.
Можно показать [1, с.21], что отношение изоморфизма между графами является отношением эквивалентности, т.е. оно симметрично, транзитивно и рефлексивно. Следовательно, оно разбивает класс всех графов на непустые и попарно непересекающиеся подклассы, называемые классами изоморфизма или классами изоморфных графов. Два произвольных графа принадлежат одному и тому же классу изоморфизма тогда и только тогда, когда они изоморфны друг другу.
Изоморфные графы естественно отождествлять, т.е. считать совпадающими (их можно изобразить одним рисунком). Они могли бы различаться конкретной природой своих элементов, но именно это игнорируется при введении понятия "граф".
Математическая теория графов интересуется такими свойствами графов, которые инвариантны относительно изоморфизма (например, числом вершин в графе, числом петель или числом вершин данной валентности и т.д.). Для специалиста по теории графов естественно отождествлять изоморфные графы. Поэтому обычно речь идет о классах изоморфизма (называемых также абстрактными графами).
Вопрос о том, изоморфны ли два данных графа, в общем случае оказывается сложным (см., например, [2]).
Для изоморфизма двух n-вершинных графов само определение этого отношения дает теоретически безукоризненный способ проверки: надо просмотреть все n! взаимно однозначных соответствий между множествами вершин и установить, совмещаются ли полностью ребра графа хотя бы при одном соответствии. Однако даже весьма грубая оценка показывает, что такое решение задачи "в лоб" практически непригодно: уже при n=20 перебор всех n! вариантов потребовал бы около 40 лет машинного времени.
Подобная ситуация, естественно, толкнула многих математиков на классический путь: попытаться найти такой инвариант (число или систему чисел), который бы, с одной стороны, легко вычислялся по заданному графу (и по возможности имел наглядный смысл), а с другой - обладал свойством полноты, т.е. определял граф однозначно с точностью до изоморфизма.
Вначале естественно поставить вопрос: какие характеристики графов инвариантны относительно изоморфизма [3,с.21]?
Примеры таких инвариантов графа G известны: это число вершин n(G), число ребер m(G) и вектор степеней s(G)=(s1, s2, ...,sn), который, в частности, дает числовые инварианты
min si и max si
i принадлежит {1,2,...,n} i принадлежит {1,2,...,n}
- Определение 2.
- Пусть f - функция, относящая каждому графу G некоторый элемент f(G) из множества M произвольной природы. Эту функцию мы будем называть инвариантом, если на изоморфных графах ее значения совпадают, т.е. для любых G и G' из изоморфности графов G и G' следует f(G)=f(G').
Введем несколько наиболее важных инвариантов графа [3, с.21-25]:
- плотность f(G) - число вершин клики графа G. Инвариантность этой характеристики следует из того, что при изоморфном соответствии двух графов каждому подмножеству вершин одного графа, порождающему клику, соответствует в другом графе подмножество с тем же числом вершин и тоже порождающее клику;
- неплотность e(G) - это наибольшее количество попарно несмежных вершин графа;
- xроматическое число g(G);
- число компонент связности K(G);
- число Хадвигера h(G).
Заметим, что матрица смежностей не является инвариантом графа: при переходе от одной нумерации его вершин к другой она претерпевает перестановку рядов, состоящую из некоторой перестановки строк и точно такой же перестановки столбцов. Любая функция от элементов aij матрицы, не меняющаяся ни при каких перестановках рядов матрицы смежности, является инвариантом графа G. К числу таких функций относятся сумма всех элементов, неупорядоченный набор сумм элементов каждой строки или сумм элементов каждого столбца, определитель матрицы, ее характеристический многочлен и корни последнего и др.
- Определение 3 [3, с.41-42].
- Инвариант f называется полным, если для любых графов G и G' из равенства f(G)=f(G') следует изоморфизм графов G и G'.
Из рассмотренных инвариантов, которые отнесены к "легко вычислимым", даже наиболее "богатый" - вектор степеней s(G) - не является полным. В процессе развития теории графов не было нехватки в гипотезах полноты или иного "трудно вычислимого" инварианта, но все эти гипотезы рано или поздно опровергались конкретными примерами.
- Определение 4.
- Степенью s вершины v графа (V,E) называется число его вершин, смежных с v, или, что то же, число ребер, инцидентных этой вершине.
Ясно, что при всяком изоморфизме графов L и L' соответствующие друг другу вершины должны иметь одинаковую степень.
- Определение 5 [3,с.17].
- Пусть G=(V,E) - n-вершинный граф, а s1, s2, ...,sn - степени его вершин, выписанные в порядке
неубывания: s1 <= s2 <= ... <= sn.
Упорядоченную систему (s1, s2, ...,sn) будем называть вектором степеней графа G и кратко обозначать s(G).
Вместо самого вектора степеней часто пользуются его обращением t(G)=(t1, t2, ...,tn), где ti=sn-i (i=1,2,...,n) - те же степени вершин, но расположенные в порядке невозрастания: t1 >= t2 >= ... >= tn.
Из сказанного выше следует, что для изоморфизма графов G и G' необходимо совпадение векторов их степеней: s(G)=s(G').
Однако достаточным это условие не является: на рисунке 1 мы видим две пары неизоморфных графов с одинаковыми векторами: s = (1,2,2,2,2,3):
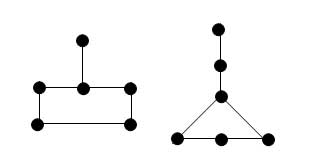
Рис.1. Пара неизоморфных графов
Не будучи идеальным средством распознавания изоморфизма, вектор степеней может тем не менее во многих случаях оказать существенную помощь.
Во-первых, если s(G) не равно s(G'), то отсюда сразу следует неизоморфность графов G и G'.
Во-вторых, если s(G)=s(G'), то для проверки графов G и G' на изоморфизм требуется перебор не всех n! соответствий между вершинами, а лишь тех, при которых сопоставляются вершины одинаковой степени. Так в примере надо перебрать лишь 4!=24 соответствия вместо 720 [3,с.17].
Пример. Распознавание изоморфизма неориентированных графов с помощью анализа вектора степеней. Результатом работы программы являются все взаимно-однозначные отоб 1ражения множества вершин первого графа на множество вершин второго графа, определяющие изоморфизм.
В программе существенным образом использован модификация алгоритма Джонсона и Троттера генерирования всех перестановок с минимальным числом транспозиций соседних элементов.
#include <iostream.h> #define TRUE 1 #define FALSE 0 #define M 10 //Максимальное количество вершин в графе. typedef int Boolean; typedef struct L *Lref; // Тип: указатель на заголовочный узел. typedef struct T *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. }; //Описание типа дугового узла. typedef struct T { Lref Id; Tref Next; }; class Spisok { private: Lref Head; //Указатель на голову списка заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент // в конце списка заголовочных узлов. int Fun[M+1]; //Массив вершин графа. int NewFun[M+1]; //Массив перестановок элементов массива Fun. void SearchGraph (int, Lref *); Lref Search(int); Boolean Find_Arc (int, int); Boolean Isomorph (Spisok, int); public: Spisok() {//Инициализация списка заголовочных узлов. Head = Tail = new (L); } Lref GetHead() { return Head; } Lref GetTail() { return Tail; } void MakeGraph (); void PrintGraph (); void Sorting (); friend void Reshenie(Spisok,Spisok); }; void main () { Spisok A,B; //Построение графов и вывод их структур смежности. A.MakeGraph (); A.PrintGraph (); cout<<endl; B.MakeGraph (); B.PrintGraph (); cout<<endl; A.Sorting (); A.PrintGraph (); cout<<endl; B.Sorting (); B.PrintGraph (); cout<<endl; //Решение. Reshenie(A,B); } void Reshenie(Spisok A, Spisok B) //Решение задачи. { Lref Ukaz; //Рабочий указатель для перемещения // по списку заголовочных звеньев. int P[M+1]; //Массив для перестановок. int Ves[M+1]; //Массив "весов" элементов массива P //(в нем хранятся степени вершин). int Ves1[M+1]; //Вначале - копия массива Ves, //затем - рабочий массив. Boolean Fl; //Флаг совпадения массивов Ves и Ves1. Boolean PR[M+1]; int C[M+1]; int x,k,t; //Определение количества вершин и функций. int N=0; Ukaz = A.GetHead(); while (Ukaz!=A.GetTail()) { N++; A.Fun[N] = A.NewFun[N] = Ukaz->Key; Ves[N] = Ukaz->Count; Ves1[N] = Ves[N]; Ukaz = Ukaz->Next; } N=0; Ukaz = B.GetHead(); while (Ukaz!=B.GetTail()) { N++; B.Fun[N] = Ukaz->Key; Ukaz = Ukaz->Next; } for (int i=1;i<=N;i++) cout << Ves[i] << " "; cout << endl; for (i=1;i<=N;i++) cout << A.Fun[i] << " "; cout << endl; for (i=1;i<=N;i++) cout << B.Fun[i] << " "; cout << endl; //Инициализация. for (i=1;i<=N;i++) { P[i] = i; C[i] = 1; PR[i] = TRUE; } //Нахождение перестановок. C[N] = 0; cout << "Отображение вершин, определяющее изоморфизм: \n"; if ( A.Isomorph (B,N) ) { for(int j=1;j<=N;j++) A.NewFun[j] = A.Fun[P[j]]; for(j=1;j<=N;j++) cout << A.NewFun[j] << " "; cout << endl; for(j=1;j<=N;j++) cout << B.Fun[j] << " "; cout << endl; } cout << " --------------------------- \n"; i = 1; while ( i<N ) { i = 1; x = 0; while ( C[i]==N-i+1 ) { PR[i] = (!PR[i]); C[i] = 1; if ( PR[i]) x++; i++; } if ( i<N ) //Выполнение транспозиции. { if ( PR[i] ) k = C[i] + x; else k = N - i + 1 - C[i] + x; t = P[k]; P[k] = P[k+1]; P[k+1] = t; t = Ves1[k]; Ves1[k] = Ves1[k+1]; Ves1[k+1] = t; C[i] += 1; //Отбор нужной перестановки. Fl = TRUE; for (int j=1;j<=N;j++) Fl = (Fl && (Ves[j]==Ves1[j])); if ( Fl ) { for (j=1;j<=N;j++) A.NewFun[j] = A.Fun[P[j]]; if (A.Isomorph (B,N)) { for (j=1;j<=N;j++) cout << A.NewFun[j] << " "; cout << endl; for (j=1;j<=N;j++) cout << B.Fun[j] << " "; cout << endl; cout << " --------------------------- \n"; } } } } } Lref Spisok::Search (int w) //Функция возвращает указатель на заголовочный узел //ключом w. Если узел отсутствует, то функция возвращает NULL . { Lref h = Head; (*Tail).Key = w; //Поиск "с барьером". while ((*h).Key!=w) h = (*h).Next; if (h==Tail) //В списке заголовочных узлов нет узла с ключом w. h = NULL; return h; } void Spisok::SearchGraph (int w, Lref *h) //Функция возвращает указатель на заголовочный узел //с ключом w в графе, заданном структурой Вирта с указателем Head. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (L); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x, &p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (T); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<< "(" << (*p).Count << ")" << (*p).Key << "("; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } } Boolean Spisok::Find_Arc (int x, int y) //Функция возвращает TRUE, если в графе, представленном //структурой Вирта (Head,Tail), существует дуга (x,y). { Lref p,q; //Рабочие указатели. Tref r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. //Определим, существует ли в графе дуга (x,y)? p = Search (x); q = Search (y); r = p->Trail; Res = FALSE; while ( r != NULL && !Res ) if (r->Id==q) Res = TRUE; else r = r->Next; return Res; } void Spisok::Sorting () //Сортировка узлов в заголовочном списке //по полю Count в порядке убывания. { Lref UkZv_1,UkZv_2; Lref UkZv_3; Tref UkZv_4; int A, B; Tref D; UkZv_1 = Head; while ( UkZv_1 != Tail ) { UkZv_2 = UkZv_1->Next; while ( UkZv_2!=Tail ) { if ( UkZv_1->Count < UkZv_2->Count ) { A = UkZv_1->Key; B = UkZv_1->Count; D = UkZv_1->Trail; UkZv_1->Key = UkZv_2->Key; UkZv_1->Count = UkZv_2->Count; UkZv_1->Trail = UkZv_2->Trail; UkZv_2->Key = A; UkZv_2->Count = B; UkZv_2->Trail = D; UkZv_3 = Head; while ( UkZv_3!=Tail ) { UkZv_4 = UkZv_3->Trail; while ( UkZv_4 != NULL ) { if ( UkZv_4->Id==UkZv_1 ) UkZv_4->Id = UkZv_2; else if ( UkZv_4->Id==UkZv_2 ) UkZv_4->Id=UkZv_1; UkZv_4 = UkZv_4->Next; } UkZv_3 = UkZv_3->Next; } } UkZv_2 = UkZv_2->Next; } UkZv_1 = UkZv_1->Next; } } Boolean Spisok::Isomorph (Spisok B, int N) //Функция, возвращающая TRUE, если графы, представленные //структурами Вирта (A.Head,A.Tail) и (B.Head,B.Tail), изоморфны. //Отображение вершин при изоморфизме задано векторами //NewFun и Fun. { Boolean Flag = TRUE; int k1,k2; for (int i=1;i<=N;i++) { k1 = 1; while ( i != this->NewFun[k1] ) k1++; for (int j=1;j<=N;j++) { k2 = 1; while ( j != this->NewFun[k2] ) k2++; if ( i>j && this->Find_Arc(i,j) ) Flag = (Flag && B.Find_Arc (B.Fun[k1],B.Fun[k2])); } } return Flag; }
Для графов, изображенных на рисунке 2,
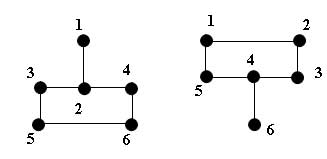
Рис.2. Пример графов
результат работы приложения будет следующим:
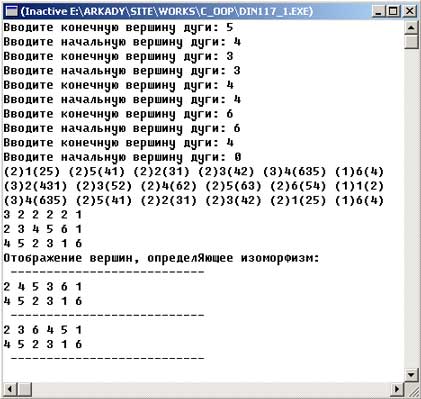
Рис.3. Результат работы приложения
Нетривиальный тестовый пример Вы можете обнаружить в монографии [4, с.207].
Однако есть случаи, когда при выяснении изоморфизма графов их векторы степеней практически бесполезны: речь идет об однородных графах, в которых степень всех вершин одна и та же.
Например, взгляните на граф, степени всех вершин которого равны 3:
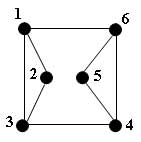
Рис.4. пример однородного графа
Противоположный случай представляют графы, определяемые однозначно с точностью до изоморфизма своим вектором степеней (или, что равносильно, его обращением) и называемые униграфами.
Алгоритм, распознавания изоморфизма графов, описанный в [5]
Этот подход используется при построении алгоритма установления изоморфизма ориентированных графов в монографии [5,с.398].
Предположим, что нам даны два ориентированных графа GX=(VX,EX) и GY=(VY, EY) и требуется выяснить, изоморфны ли они. Мы полагаем, что VX=VY={1,2,...,n}, ибо если |VX| не равно |VY|, то ориентированные графы не могут быть изоморфными.
Пусть один из ориентированных графов, скажем GX, выбран в качестве эталона. Пусть GX(k) - подграф графа GX, индуцируемый вершинами {1,2,...,k}, 0<=k<=n. Ясно, что GX(0) - пустой подграф и GX(1) - подграф, состоящий из единственной вершины 1 и не содержащий ребер.
При определении того, изоморфны ли графы GX и GY, используем технику поиска с возвращением.
Очевидно, GX(0) изоморфен пустому подграфу GY. Предположим, что на некотором шаге найден подграф GY, состоящий из вершин S, принадлежащих VY, который изоморфен GX(k).
Попытаемся продолжить изоморфизм на GX(k+1), выбирая вершину v, принадлежащую VY-S, соответствующую k+1 из VX.
Если такая вершина v найдена, то зафиксируем соответствие fk+1<-v и попытаемся продолжить изоморфизм на GX(k+2).
Если такой вершины не существует, то возвращаемся в GX(k-1) и пытаемся выбрать другую вершину, соответствующую k из VX.
Этот процесс продолжается до тех пор, пока не будет найден изоморфизм между GX(n)=GX и GY, в противном случае возвращаемся к GX(0), заключив, что графы GX и GY неизоморфны.
С.Гудман и С.Хидетниеми [6,с.62] предложили называть эвристическим алгоритм, который обладает следующими двумя свойствами:
- Он находит, как правило, хорошие, хотя и не обязательно оптимальные решения.
- Его легче и быстрее реализовать, чем любой из известных точных алгоритмов (т.е. алгоритмов, гарантирующих оптимальное решение).
Эвристики для решения задач изоморфизма обычно состоят в попытках показать, что рассматриваемые графы не изоморфны. Для этого составляется список различных инвариантов в порядке, определяемом сложностью вычисления инварианта. Затем последовательно сравниваются значения параметров данных графов. Как только обнаруживаются два различных значения одного и того же параметра, приходят к заключению, что данные графы неизоморфны.
Рассмотрим пример достаточно сложной эвристики, работающей с матрицей смежности A(G) [6, с.63-64].
Алгоритм сравнения порядков смежности
Вычисляется A2(Gi) для i=1, 2. Затем переставляются строки и столбцы A2(G1) и A2(G2) так, чтобы элементы на главной диагонали оказались в нисходящем порядке.
Если G1 и G2 изоморфны и все диагональные элементы различны, то при этой перестановке должны получиться идентичные матрицы.
Если нет, то данные два графа не могут быть изоморфными.
Если матрицы идентичны, то можно продолжить проверку с A3(Gi), A4(Gi), ..., Ak(Gi) для i=1, 2. Значение k определяется имеющимся бюджетом машинных ресурсов. Если все из проверенных матриц совпадают, то весьма правдоподобно, но не обязательно истинно, что G1 и G2 изоморфны.
Замечания.
- Графы изоморфны тогда и только тогда, когда их матрицы смежностей
получаются друг из друга одинаковыми перестановками строк и столбцов [7,с.28].
Графы (ориентированные графы) изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга произвольными перестановками строк и столбцов [7, с.28].
- Существует немало глубоких и трудных проблем, связанных с изоморфизмом графов, и наиболее известная из них - проблема восстановления.
Пусть вершины графа G занумерованы следующим образом: v1, v2, ...,vk. Через Gj обозначим граф, получающийся из G после удаления вершины vj и инцидентных ей ребер. Все k подграфов Gj 0 графа G будем называть примарными [1, с.154].
C1 (гипотеза о восстановлении).
Если заданы классы изоморфизма всех k примарных подграфов графа G, то при k>=3 класс изоморфизма графа G определяется однозначно.
К моменту написания книги У.Татта [1] гипотеза о восстановлении оставалась недоказанной.
Ограничение на k (k>=3) обосновывается легко.
Если k=1, то единственным примарным подграфом графа G будет пустой граф, который не несет никакой информации о числе петель в графе G. Если k=2, то в каждом из двух примарных подграфов графа G содержится только по одной вершине, а потому нам ничего не известно о числе ребер в графе G. Таким образом, действительно нужно предположить, что |V(G)|>=3.
Если некоторое свойство или характеристику графа G можно выявить, рассматривая классы изоморфизма всех его примарных подграфов Gj, то оно (она) называется восстанавливаемым (восстанавливаемой), а графы, обладающие этим свойством или характеристикой, называются распознаваемыми. Примером восстанавливаемой характеристики является число вершин в графе. Это число на единицу больше числа вершин в каждом примарном подграфе данного графа и совпадает с числом заданных классов изоморфизма.
Пусть G - граф с занумерованными ребрами A1, A2, ...,Ak. Через Gj обозначим подграф графа G, получающийся после удаления из G ребра Aj.
C2 (гипотеза о реберном восстановлении).
Если заданы классы изоморфизма всех k подграфов Gj, то при k>=4 класс изоморфизма графа G определяется однозначно.
Причина, по которой введено ограничение на k (k>=4) ясна из следующего рисунка [1, с.164], на котором изображены два графа G и H, такие, что, удаляя из них произвольное ребро, мы получаем, с точностью до изоморфизма, один и тот же подграф.
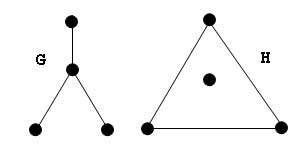
Рис.5. Пример графов - [7, с.14]. В некоторых ситуациях все же приходится различать изоморфные графы,
и тогда полезно понятие "помеченный граф". Граф порядка n называется помеченным, если его вершинам присвоены некоторые метки, например,
номера 1, 2, ..., n.
Отождествив каждую из вершин графа с ее номером (и, следовательно, множество вершин - с множеством чисел {1, 2, ..., n}), определим равенство помеченных графов G и H одного и того же порядка: G=H тогда, когда множество ребер графа G совпадает с множеством ребер графа H.
(1) Татт У. Теория графов. - М.: Мир, 1988. - 424 с.
(2) Земляченко В.Н., Корнеенко Н.М., Тышкевич Р.И. Проблема изоморфизма графов // Теория сложности вычислений, I. Записки научных семинаров ЛОМИ. - 1982. - Т.118. - С.83-158.
(3) Зыков А.А. Основы теории графов. М.: Наука, 1987. - 384 с.
(4) Белов В.В., Воробьев Е.М., Шаталов В.Е. Теория графов. - М.: Высш.шк., 1976. - 392 с.
(5) Рейнгольд Э., Hивергельт Ю., Део H. Комбинаторные алгоритмы. Теория и практика. - М.: Мир, 1980. - 476 с.
(6) Гудман С., Хидетниеми С. Введение в разработку и анализ алгоритмов. - М.: Мир, 1981. - 368 с.
(7) Лекции по теории графов / Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. - М.: Наука, 1990. - 384 с.
Со следующего шага мы начнем краткий обзор сетей.
