Шаг 116.
Алгоритмы раскраски графа

    На этом шаге мы рассмотрим алгоритмы закраски графа.

    Задачи определения хроматического числа и построения минимальной раскраски произвольного графа являются очень сложными. С одной стороны, не известны алгоритмы их решения, сложность которых есть некоторая фиксированная степень от длины записи условий задачи (так называемые полиномиальные алгоритмы). С другой стороны, нигде явно не выражены те потери, которые мы несем от отсутствия таких алгоритмов [1, с.70].

    Разумеется, есть лишь конечное число ситуаций, которые надо рассмотреть, чтобы найти хроматическое число n-вершинного графа. Действительно, всего имеется kn различных способов раскраски графа G в k цветов. Перебрав их, мы либо найдем правильную раскраску G в k цветов, либо убедимся, что таковой не существует. Ясно, что это самый примитивный способ решения задачи. Имеется целый ряд значительно более совершенных методов, использующих как оценки, так и другие соображения, призванные сократить перебор.

    Рассмотрим простой алгоритм построения правильной раскраски [2, с.237], в ряде случаев приводящий к раскраскам, близким к минимальным.

   

Алгоритм последовательной раскраски

  1. Произвольной вершине v1 графа G припишем цвет 1.
  2. Если вершины v1, v2, ...,vi раскрашены l цветами 1, 2, ..., l, l<=i, то новой произвольно взятой вершине vi+1 припишем минимальный цвет, не использованный при раскраске смежных вершин.

    Приведем реализацию алгоритма, осуществляющего последовательную раскраску вершин графа при помощи обхода графа в глубину.

    Пример 1. 
//Последовательная раскраска вершин графа при помощи
//обхода графа в глубину.        
//Граф представлен структурой Вирта.
#include <iostream.h>
#define TRUE 1
#define FALSE 0
typedef int Boolean;
typedef struct L *Lref; // Тип: указатель на заголовочный узел.
typedef struct T *Tref; // Тип: указатель на дуговой узел.

//Описание типа заголовочного узла.
typedef struct L 
{ 
  int Key; //Имя заголовочного узла.
  int Color; //Цвет раскраски.
  int Count; //Количество предшественников.
  Boolean Flag; //Флаг посещения узла при обходе.
  Tref Trail; //Указатель на список смежности.
  Lref Next; //Указатель на следующий узел в списке заголовочных узлов.
};

//Описание типа дугового узла.
typedef struct T 
{ 
  Lref Id; 
  Tref Next; 
};

class Spisok
{
  private:
    Lref Head; //Указатель на голову списка заголовочных узлов.
    Lref Tail; //Указатель на фиктивный элемент 
               // в конце списка заголовочных узлов.
    int MSet[256]; //Вспомогательное множество, содер- 
                   //жащее 0,1,2...,n.
    void SearchGraph (int, Lref *);
  public:
    Spisok() {//Инициализация списка заголовочных узлов.
              Head = Tail =  new (L); }
    Lref GetHead() { return Head; }
    Lref GetTail() { return Tail; }
    void MakeGraph ();
    void PrintGraph ();
    void Color (Lref, int);
    void Postr (int);
};

void main ()
{
  Spisok A;
  Lref t; //Рабочий указатель для перемещения 
          // по списку заголовочных звеньев.
  int n=0; //Количество вершин в графе.

  //Построение графа и вывод его структуры Вирта.
  A.MakeGraph ();
  A.PrintGraph (); cout<<endl;
  //Раскраска с помощью рекурсивного обхода графа в глубину.
  //Инициализация.
  t = A.GetHead(); //Установлен рабочий указатель.
  while (t!=A.GetTail())
    { t->Flag = TRUE; t->Color = 0;
      n++; t = (*t).Next; }
  // ------------------------------------ 
  //Построение вспомогательного множества MSet.
  A.Postr(n);
  cout << "Результат раскраски: "; 
  A.Color (A.GetHead(),n);
  cout << endl;
} 

void Spisok::Postr (int n)
//Построение вспомогательного множества MSet.
{
  for (int i=0;i<256;i++)
    MSet[i] = (i<=n)?1:0;
}

void Spisok::SearchGraph (int w, Lref *h)
//Функция возвращает указатель на заголовочный узел 
//с ключом w в графе, заданном структурой Вирта с указателем Head. 
{
  *h = Head; (*Tail).Key = w;
  while ((**h).Key!=w) *h = (**h).Next;
  if (*h==Tail)
  //В списке заголовочных узлов нет узла с ключом w.
  //Поместим его в конец списка Head.
  { Tail = new (L); (**h).Count = 0; 
    (**h).Trail = NULL; (**h).Next = Tail; }
}

void Spisok::MakeGraph ()
//Функция возвращает указатель Head на структуру 
//Вирта, соответствующую ориентированному графу.
{
  int x,y;
  Lref p,q; //Рабочие указатели.
  Tref t,r; //Рабочие указатели.
  Boolean Res; //Флаг наличия дуги.
  cout<<"Вводите начальную вершину дуги: ";
  cin>>x;
  while (x!=0)
  {
     cout<<"Вводите конечную вершину дуги: "; cin>>y;
     //Определим, существует ли в графе дуга (x,y)?
     SearchGraph (x, &p); SearchGraph (y,&q);
     r = (*p).Trail; Res = FALSE; 
     while ((r!=NULL)&&(!Res)) 
       if ((*r).Id==q) Res = TRUE; 
       else r = (*r).Next; 
     if (!Res) //Если дуга отсутствует, то поместим её в граф.
      { t = new (T); (*t).Id = q; 
        (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } 
     cout<<"Вводите начальную вершину дуги: "; cin>>x;
  }
}

void Spisok::PrintGraph ()
//Вывод структуры Вирта, заданной указателем 
//Head и соответствующей ориентированному графу.
{
  Lref p; //Рабочий указатель.
  Tref q; //Рабочий указатель.

  p = Head;
  while (p!=Tail)
  {
     cout<< (*p).Key << "("; q = (*p).Trail; 
     while (q!=NULL) 
      { cout<<(*(*q).Id).Key; q = (*q).Next; } 
     cout<<")"; p = (*p).Next; cout<<" ";
  }
}

void Spisok::Color (Lref r, int n)
//Последовательная раскраска графа при помощи
//рекурсивного обхода графа в глубину.
//r - указатель на структуру Вирта.
//MSet - глобальное множество.
//n    - количество вершин в графе.
{
  Tref t,t1;
  int i;         //Параметр цикла.
  Boolean Fl;

  t = r->Trail; r->Flag = FALSE;
  //Сейчас мы находимся в вершине r->Key.
  //Исключим цвета всех вершин, смежных вершине
  //r->Key, из множества MSet.
  t1 = t;
  while ( t1 != NULL )
  {  MSet[t1->Id->Color] = 0; t1 = t1->Next; }
  //Выбор цвета вершины: это "первый" элемент множества MSet.
  Fl = TRUE; i = 1;
  while ( Fl )
   if ( MSet[i] ) Fl = FALSE; else  i++;
  r->Color = i;   //Цвет присвоен!
  cout << "(" << r->Key << "," << r->Color << ") ";
  //Восстановление вспомогательного множества MSet.
  for (i=0;i<256;MSet[i++]=0);
  for (i=0;i<=n;MSet[i++]=1);
  // ------------- 
  while ( t != NULL )
  {  
    if ( t->Id->Flag ) Color (t->Id,n);
    t = t->Next;
  }
}
Текст этой программы можно взять здесь.

    Приведем реализацию алгоритма, осуществляющего последовательную раскраску вершин графа при помощи обхода графа в ширину. 

//Последовательная раскраска графа при помощи
//обхода графа в ширину. 
//Граф представлен структурой Вирта.
#include <iostream.h>
#define TRUE 1
#define FALSE 0
typedef int Boolean;
typedef struct Leader *Lref; // Тип: указатель на заголовочный узел.
typedef struct Trailer *Tref; // Тип: указатель на дуговой узел.

//Описание типа заголовочного узла.
typedef struct Leader 
{ 
  int Key; //Имя заголовочного узла.
  int Count; //Количество предшественников.
  int Color; //Цвет раскраски.
  Boolean Flag; //Флаг посещения узла при обходе.
  Tref Trail; //Указатель на список смежности.
  Lref Next; //Указатель на следующий узел в списке заголовочных узлов.
};

//Описание типа дугового узла.
typedef struct Trailer
{
  Lref Id;
  Tref Next;
};

//Описание типа узла очереди.
typedef Lref TipElement; //Указатель на звено заголовочного списка.
typedef struct Zveno *svqz;
typedef struct Zveno
{
  TipElement Element; //Указатель на список смежности.
  svqz Sled;
};

class Spisok
{
  private:
     Lref Head; //Указатель на голову списка заголовочных узлов.
     Lref Tail; //Указатель на фиктивный элемент
                // в конце списка заголовочных узлов.
     int MSet[256]; //Вспомогательное множество, содер- 
                    //жащее 0,1,2...,n.
     void Udalenie_A (svqz *, svqz *, TipElement *);
     void Dobavlenie (svqz *, svqz *, TipElement);
     void SearchGraph (int, Lref *);
  public:
     Spisok() {//Инициализация списка заголовочных узлов.
                Head = Tail =  new (Leader); }
     Lref GetHead() { return Head; }
     Lref GetTail() { return Tail; }
     void MakeGraph ();
     void PrintGraph ();
     void Color (Lref, int);
     void Postr (int);
};

void main ()
{
  Spisok A;
  Lref t; //Рабочий указатель для перемещения 
          // по списку заголовочных звеньев.
  int n=0; //Количество вершин в графе.

  //Построение графа и вывод его структуры Вирта.
  A.MakeGraph ();
  A.PrintGraph (); cout<<endl;
  //Раскраска с помощью рекурсивного обхода графа в ширину.
  //Инициализация.
  t = A.GetHead(); //Установлен рабочий указатель.
  while (t!=A.GetTail())
    { t->Flag = TRUE; t->Color = 0;
      n++; t = (*t).Next; }
  // ------------------------------------ 
  //Построение вспомогательного множества MSet.
  A.Postr(n);
  cout << "Результат раскраски: "; 
  A.Color (A.GetHead(),n);
  cout << endl;
}

void Spisok::Postr (int n)
//Построение вспомогательного множества MSet.
{
  for (int i=0;i<256;i++)
    MSet[i] = (i<=n)?1:0;
}

void Spisok::SearchGraph (int w, Lref *h)
//Функция возвращает указатель на заголовочный узел
//с ключом w в графе, заданном структурой Вирта с указателем Head.
{
  *h = Head; (*Tail).Key = w;
  while ((**h).Key!=w) *h = (**h).Next;
  if (*h==Tail)
  //В списке заголовочных узлов нет узла с ключом w.
  //Поместим его в конец списка Head.
  { Tail = new (Leader); (**h).Count = 0;
	 (**h).Trail = NULL; (**h).Next = Tail; }
}

void Spisok::MakeGraph ()
//Функция возвращает указатель Head на структуру
//Вирта, соответствующую ориентированному графу.
{
  int x,y;
  Lref p,q; //Рабочие указатели.
  Tref t,r; //Рабочие указатели.
  Boolean Res; //Флаг наличия дуги.
  cout<<"Вводите начальную вершину дуги: ";
  cin>>x;
  while (x!=0)
  {
	  cout<<"Вводите конечную вершину дуги: "; cin>>y;
	  //Определим, существует ли в графе дуга (x,y)?
	  SearchGraph (x, &p); SearchGraph (y,&q);
	  r = (*p).Trail; Res = FALSE;
	  while ((r!=NULL)&&(!Res))
		 if ((*r).Id==q) Res = TRUE;
		 else r = (*r).Next;
	  if (!Res) //Если дуга отсутствует, то поместим её в граф.
		{ t = new (Trailer); (*t).Id = q;
		  (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; }
	  cout<<"Вводите начальную вершину дуги: "; cin>>x;
  }
}

void Spisok::PrintGraph ()
//Вывод структуры Вирта, заданной указателем
//Head и соответствующей ориентированному графу.
{
  Lref p; //Рабочий указатель.
  Tref q; //Рабочий указатель.

  p = Head;
  while (p!=Tail)
  {
	  cout<<(*p).Key<<"("; q = (*p).Trail;
	  while (q!=NULL)
		{ cout<<(*(*q).Id).Key; q = (*q).Next; }
	  cout<<")"; p = (*p).Next; cout<<" ";
  }
}

void Spisok::Dobavlenie (svqz *L, svqz *R, TipElement elem)
//Добавление элемента elem в очередь, заданную указателями L и R.
{
  svqz K = new (Zveno);

  K->Element = elem; K->Sled = NULL;
  if (*L==NULL)
	 { (*L) = K; (*R) = K; }
  else { (*R)->Sled = K; (*R) = K; }
}

void Spisok::Udalenie_A (svqz *L, svqz *R, TipElement *A)
//Удаление элемента из очереди, заданной указателями L и R и
//помещение удаленного элемента в переменную A.
{
  svqz q;

  if ((*L)!=NULL)
   if ((*L)->Sled!=NULL)
   {
     (*A) = (*L)->Element; q = (*L);
     (*L) = (*L)->Sled; delete q;
   }
   else {
         (*A) = (*L)->Element; delete *L;
         (*L) = (*R) = NULL;
        }
}

void Spisok::Color (Lref H, int n)
//Последовательная раскраска графа при помощи обхода графа
//в ширину, начиная с вершины, заданной указателем H
//(нерекурсивный обход).
{
  svqz L;   // Указатель на начало очереди.
  svqz R;   // Указатель на конец  очереди.
  Lref p;   // Рабочий указатель.
  Tref t;   // Рабочий указатель.
  Tref t1;
  int i;    // Параметр цикла.
  Boolean Fl;

  L = R = NULL; // Создание пустой очереди.
  Dobavlenie (&L,&R,H); H->Flag = FALSE;
  while ( L != NULL )
  {  //Пока очередь не пуста...
     Udalenie_A (&L,&R,&p);
     t = p->Trail;
     //Сейчас мы находимся в вершине r->Key.
     //Исключим цвета всех вершин, смежных вершине 
     //r->Key, из множества MSet.
     t1 = t;
     while ( t1 != NULL )
     {  MSet[t1->Id->Color] = 0; t1 = t1->Next; }
     //Выбор цвета вершины - "первого" элемента множества MSet.
     Fl = TRUE; i = 1;
     while ( Fl )
      if ( MSet[i] ) Fl = FALSE; else  i++;
     p->Color = i;   //Цвет присвоен!
     cout << "(" << p->Key << "," << p->Color << ") ";
     //Восстановление вспомогательного множества MSet.
     for (i=0;i<256;MSet[i++]=0);
     for (i=0;i<=n;MSet[i++]=1);
     while ( t != NULL )
     {
       if ( t->Id->Flag )
       {
          Dobavlenie (&L,&R,t->Id);
          t->Id->Flag = FALSE;
       }
       t = t->Next;
     }
  }
}
Текст этой программы можно взять здесь.

    Пример 3. 
//Последовательная раскраска графа, представленного с помощью
//модифицированных списков смежности.
#include <iostream.h>
#include <conio.h>
#define TRUE 1
#define FALSE 0
#define XRY 8  //Количество вершин графа.
typedef int Boolean;
typedef struct zveno *svqz;
typedef struct zveno
{
  int Key;  // Вершина графа.
  svqz Up;  // Указатель на смежную вершину.
  svqz Sled;// Указатель на следующую смежную вершину.
};

class Spisok
{
  private:
     svqz Beg[XRY+1]; //Массив указателей на вершины.
     void Add_Ver (int);
     int Find (int, int, svqz *);
     void Add_duga (int, int);
     void Make (int, int);
     void Delinenok (int, int);
     void Del_Duga (int, int);
     void Del_Ver (int);
     int Find_Color (int, int, svqz *);
  public:
     Spisok();
     void Init_Graph ();
     void Make_Graph ();
     void Print_Graph ();
     void Color ();
     void Print_Color ();
};

void main ()
{
  Spisok A;

  //Инициализация графа.
  A.Init_Graph ();
  //Построение графа.
  A.Make_Graph ();
  //Вывод графа.
  A.Print_Graph ();
  getch();
  //Последовательная раскраска графа, представленного
  //модифицированными списками смежности.
  A.Color ();
  A.Print_Color (); 
  getch();
}

Spisok::Spisok()
{
  for ( int i=0; i<=XRY;Beg[i++] = NULL );
}

void Spisok::Add_Ver (int x)
//Функция создания вершины x.
{
  svqz Ukaz = new (zveno);

  Ukaz->Sled = NULL; 
  Beg[x] = Ukaz;
}

void Spisok::Init_Graph ()
//Функция инициализации модифицированных списков смежности.
{
  for (int i=1;i<=XRY;i++) Add_Ver (i);
}

int Spisok::Find (int x, int y, svqz *UkZv)
//Функция проверки смежности вершин y и x. Функция возвращает
//TRUE, если  вершина x смежна с вершиной y. Указатель *UkZv,
//возвращает указатель на место y в списке  смежности x. Если
//вершина x не смежна с вершиной y, то UkZv есть NULL.
{
  svqz Ukaz;

  Ukaz = Beg[x]->Sled;
  while  (Ukaz != NULL && Ukaz->Key != y) 
     Ukaz = Ukaz->Sled;
  *UkZv = Ukaz;
  return  ( Ukaz != NULL );
}

void Spisok::Add_duga (int x, int y)
//Функция создания дуги (x,y).
{
  svqz Ukaz = new (zveno);

   Ukaz->Sled = Beg[x]->Sled; Ukaz->Key = y;
   Beg[x]->Sled = Ukaz;
}

void Spisok::Make (int x, int y)
//Функция создания ребра {x,y}.
{
  svqz Ukaz;

  if  ( !Find(x,y,&Ukaz) )
  {
     Add_duga (x,y);
     if ( x != y ) Add_duga (y,x);
     Beg[x]->Sled->Up = Beg[y];
     Beg[y]->Sled->Up = Beg[x];
  }
}

void Spisok::Make_Graph ()
//Функция построения модифицированных списков смежности.
{
  int f;
   
  for (int i=1;i<=XRY;i++)
  {
    cout << "Введите вершины, смежные с " << i << "-й вершиной: ";
    cin >> f;
    while (f!=0)
    {
      Make (i,f); 
      cout << " "; 
      cin >> f;
    }
    cout << endl;
  }
}

void Spisok::Delinenok (int x, int y)
//Функция удаления дуги (x,y).
{
  svqz Ukaz;
  svqz Ukazlenok;
  
  Ukazlenok = Beg[x]; Ukaz = Beg[x]->Sled;
  while (Ukaz != NULL && Ukaz->Key != y)
  {  Ukazlenok = Ukaz; Ukaz = Ukaz->Sled; }
  if ( Ukaz != NULL )
  {
     Ukazlenok->Sled = Ukaz->Sled;
     delete Ukaz;
  }
}

void Spisok::Del_Duga (int x, int y)
//Функция удаления ребра {x,y}.
{
  Delinenok (x,y); Delinenok (y,x);
}

void Spisok::Del_Ver (int x)
//Функция удаления вершины x.
{
  svqz Ukaz;
  svqz Ukazlenok;

  for (int i=1;i<=XRY;i++) Delinenok (i,x);
  Ukaz = Beg[x]; Beg[x] = NULL;
  while ( Ukaz != NULL )
  {
     Ukazlenok = Ukaz->Sled;
     delete Ukaz; Ukaz = Ukazlenok;
  }
}

void Spisok::Print_Graph ()
//Функция вывода содеpжимого модифицированных
//списков смежности.
{
  svqz UkZv;
  
  for (int i=1;i<=XRY;i++)
  {
    if ( Beg[i] != NULL )
    {
      UkZv = Beg[i]->Sled;
      cout << i << " - ";
      while ( UkZv != NULL )
      {
        cout << " " << UkZv->Key;
        UkZv = UkZv->Sled;
      }
    }
    cout << endl;
  }
}

int Spisok::Find_Color (int x, int c, svqz *UkZv)
//Функция  выявления возможности раскраски вершины  x цветом c. 
//Функция  возвращает TRUE, если вершину  x  можно  раскрасить. 
//Указатель *UkZv, возвращает указатель на вершину, смежную с x 
//и раскрашенную цветом c. Если вершину x можно раскрасить, то 
//*UkZv есть NULL.
{
   int i = 1;
   
   while (!(Find(x,i,&(*UkZv)) &&
          Beg[i]->Key==c)   && 
          i != x) i++;
   return (i==x);
}

void Spisok::Color ()
//Функция последовательной раскраски графа, заданного
//модифицированными списками смежности Beg.
{
  int i = 1;
  int c = 1;
  svqz UkZv;
   
  while  (Beg[i] == NULL && i<=XRY) i++;
  if ( i != XRY )
  {
    Beg[i]->Key = c;
    i++;
    while  (i<=XRY)  
     if ( Beg[i] != NULL )
     {
       c = 1;
       while  (!Find_Color(i,c,&UkZv)) c++;
       Beg[i]->Key = c; i++;
     }
     else  i++;
  }
  else  cout << "Граф отсутствует!";
}

void Spisok::Print_Color ()
//Функция вывода раскраски графа, заданного
//модифицированными списками смежности Beg.
{                 
  for (int i=1;i<=XRY;i++)
    if ( Beg[i] != NULL )
       cout << " Color " << i << " - " << Beg[i]->Key << endl;
}
Текст этой программы можно взять здесь.

    Результат работы приложения изображен на рисунке 1:


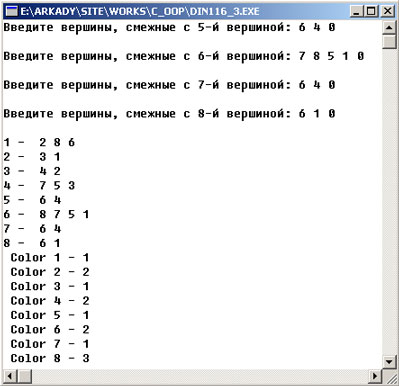
Рис.1. Результат работы приложения

    Отметим, что для некоторых классов графов (например, полных k-дольных) последовательная раскраска является минимальной [2, с.238].

    В общем случае это не так!

   

Алгоритм прямого неявного перебора

    Приведем теперь алгоритм прямого неявного перебора для определения хроматического числа графа, использующий дерево поиска [3, с.89-90].

    Предположим, что множество вершин каким-то образом упорядочено и vi - i-я вершина этого множества.

    Вначале построим первоначальную допустимую раскраску по следующему алгоритму:

    1) окрасить v1 в цвет 1;

    2) каждую из оставшихся вершин окрашивать последовательно в соответствии с заданным упорядочением: вершина vi окрашивается в цвет с наименьшим возможным "номером" (т.е. выбираемый цвет должен быть первым в данном упорядочении цветом, не использованным при окраске какой-либо вершины, смежной с vi).

    Опишем последующие шаги алгоритма согласно монографии [3, с.89].

    Пусть q - число цветов, требуемое для вышеупомянутой раскраски. Если существует раскраска, использующая только q-1 цветов, то все вершины, окрашенные в цвет q, должны быть перекрашены в цвет j<q. Пусть vi* - первая вершина при заданном упорядочении, которая была окрашена в цвет q. Поскольку она была так окрашена потому, что не могла быть окрашена в цвет j<q, то ее можно перекрасить в цвет j     Итак, шаг возвращения из вершины vi* можно осуществить следующим образом. Из смежных с vi* вершин в множестве {x1, x2, ..., xi*-1} найти последнюю (при заданном упорядочении), т.е. вершину с наибольшим индексом. Пусть это будет вершина xk. Если xk окрашена в цвет jk, то xk перекрашивается в другой допустимый цвет с наименьшим возможным "номером" jk', таким, что jk' >= jk+1.

    Если jk'<q, то надо продолжать последовательно перекрашивать все вершины с xk+1 до xn, применяя указанное выше правило 2 и помня о том, что цвет q использовать нельзя.

    Если такая процедура осуществима, то будет найдена новая лучшая раскраска, использующая меньше, чем q цветов. В противном случае, т.е. если встретится вершина, "требующая" цвет q, то можно снова сделать шаг возвращения - из такой вершины.

    Если jk'=q или нет другого допустимого цвета jk', то можно сразу же делать шаг возвращения из вершины xk.

    Алгоритм заканчивает работу, когда на шаге возвращения достигается вершина x1.

    Хотя описанная процедура неявного перебора является примитивным древовидным поиском, тем не менее она ничуть не хуже других известных методов раскраски графов [3, с.90].

    Замечание [1, с.70]. Мы не привели пока ни одного интересного примера, в котором хроматическое число выступает в роли объекта, практическая важность изучения которого несомненна. Попытаемся восполнить этот пробел.

    Задача об обслуживании авиалиний.

    Имеется некоторый город M, который связан маршрутами с городами A1, A2, ..., Am. Пусть, согласно расписанию, маршрут MAiM обслуживается в интервале времени [ai, bi]. Другими словами, ai - это тот момент, начиная с которого самолет связан с маршрутом MAiM, а bi - тот момент, когда эта связь прекращается. Таким образом, задано m временных интервалов [a1, b1], ..., [am, bm]. Требуется указать, каково минимальное число самолетов, достаточное для обслуживания всех рейсов?

    Соответствующему расписанию сопоставим граф G, вершинами которого будут заданные временные интервалы, а две вершины будут смежны тогда и только тогда, когда соответствующие интервалы имеют непустое пересечение. Этот граф и служит моделью для нашей задачи.

    Утверждение.

    Искомое число самолетов равно хроматическому числу графа G.

    Действительно, все рейсы, имеющие одинаковый цвет, могут быть обслужены одним самолетом. С другой стороны, если имеется некоторое число самолетов для обслуживания всех рейсов, то, окрасив одним цветом все рейсы, обслуживаемые одним самолетом, мы получим некоторую правильную раскраску графа G. Эти соображения и обосновывают сформулированное утверждение.

   

(1) Компьютер и задачи выбора. - М.: Наука, 1989. - 208 с.
(2) Лекции по теории графов / Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. - М.: Наука, 1990. - 384 с.
(3) Кристофидес Н. Теория графов. Алгоритмический подход. - М.: Мир, 1978. - 432 с.

    На следующем шаге мы рассмотрим изоморфизм графов.




Предыдущий шаг Содержание Следующий шаг