На этом шаге мы приведем описание алгоритма Дейкстры.

    Напомним, что алгоритм Дейкстры разработан для нахождения кратчайшего пути между заданным исходным узлом и любым другим узлом сети.

    В процессе выполнения этого алгоритма при переходе от узла i к следующему узлу j используется специальная процедура пометки ребер. Обозначим через u_i кратчайшее расстояние от исходного узла 1 до узла i, через d_ij - длину ребра (i, j). Тогда для узла j определим метку [u_j, i] следующим образом:

    [uj, i] = [ui + dij, i], dij >= 0 

    Метки узлов в алгоритме Дейкстры могут быть двух типов: временные и постоянные. Временная метка впоследствии может быть заменена на другую временную, если будет найден более короткий путь к данному узлу. Когда же станет очевидным, что не существует более короткого пути от исходного узла к данному, статус временной метки изменяется на постоянный.

    Вычислительная схема алгоритма состоит из следующих шагов.

    Шаг 0. Исходному узлу (узел 1) присваивается метка [0, -]. Полагаем i = 1.

    Шаг i. а) Вычисляются временные метки [u_i + d_ij, i] для всех узлов j, которые можно достичь непосредственно из узла i и которые не имеют постоянных меток. Если узел j уже имеет метку [u_j, k], полученную от другого узла k, и если u_i + d_ij < u_j, тогда метка [u_j, k] заменяется на [u_i + d_ij, i].

    b) Если все узлы имеют постоянные метки, процесс вычислений заканчивается. В противном случае выбирается метка [u_r, s] с наименьшим значением расстояния u_r среди всех временных меток (если таких меток несколько, то выбор произволен). Полагаем i = r и повторяем шаг i.

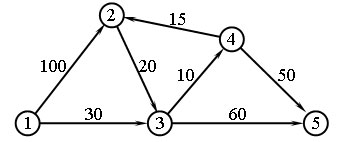
Рис.1. Транспортная сеть

    Шаг 0. Назначаем узлу 1 постоянную метку [0, -].

    Шаг 1. Из узла 1 можно достичь узлов 2 и 3. Вычисляем метки для этих узлов, в результате получаем следующую таблицу меток:

Узел	Метка		          Статус метки
  1	[0, -]                   Постоянная
  2	[0 + 100, 1] = [100, 1]  Временная
  3	[0 + 30, 1] = [30, 1]  <-Временная

    Среди узлов 2 и 3 узел 3 имеет наименьшее значение расстояния (u₃ = 30). Поэтому статус метки этого узла изменяется на "постоянная".

    Шаг 2. Из узла 3 (последнего узла с постоянной меткой) можно попасть в узлы 4 и 5. Получаем следующий список узлов:

Узел	Метка                     Статус метки
  1	[0, -]                     Постоянная
  2	[100, 1]                   Временная
  3	[30, 1]                    Постоянная
  4	[30 + 10, 3] = [40, 3]   <-Временная
  5	[30 + 60, 3] = [90, 3]     Временная

    Временный статус метки [40, 3] узла 4 заменяется на постоянный (u₄ = 40).

    Шаг 3. Из узла 4 можно достичь узлов 2 и 5. После вычисления меток получим следующий их список:

Узел	Метка	                                  Статус метки
  1	[0, -]                                    Постоянная
  2	[40 + 15, 4] = [55, 4]                  <-Временная
  3	[30, 1]                                   Постоянная
  4	[40, 3]                                   Постоянная
  5	[90, 3] или [40 + 50, 4] = [90, 4]        Временная

    Временная метка [100, 1], полученная узлом 2 на втором шаге, изменена на [55, 4]. Это указывает на то, что найден более короткий путь к этому узлу (проходящий через узел 4). На третьем шаге узел 5 получает две метки с одинаковым значением расстояния u₅ = 90.

    Шаг 4. Из узла 2 можно перейти только в узел 3, но он уже имеет постоянную метку, которую нельзя изменить. Поэтому на данном шаге получаем такой же список меток, как и на предыдущем шаге, но с единственным изменением: метка узла 2 получает статус постоянной. С временной меткой остается только узел 5, но так как из этого узла нельзя попасть ни в какой другой, процесс вычислений заканчивается.

    Алгоритм позволяет проводить вычисления непосредственно по схеме сети, как показано на рисунке 2.

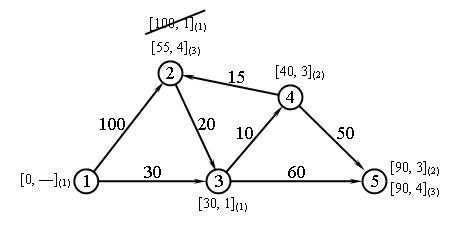
Рис.2. Вычисления по схеме (в скобках указан номер шага)

    Кратчайший маршрут между узлом 1 и любым другим узлом определяется начиная с узла назначения путем прохождения их в обратном направлении с помощью информации, представленной в постоянных метках. Например, для определения кратчайшего маршрута между узлами 1 и 2 получаем такую обратную последовательность узлов:

    (2) -> [55, 4] -> (4) -> [40, 3] -> (3) -> [30, 1] -> (1).

    Таким образом, получаем путь 1->3->4->2 общей длиной 55 километров.

    Проиллюстрируем описанный алгоритм программой, приведенной на 120 шаге. Для разобранного примера результат работы этой программы будет следующим:

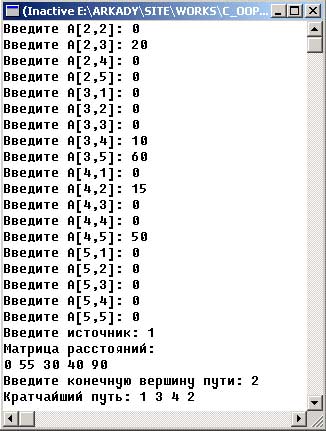
Рис.3. Результат работы приложения

    На следующем шаге мы рассмотрим алгоритм Флойда.

Предыдущий шаг Содержание Следующий шаг