На этом шаге мы реализуем алгоритм нахождения максимального потока.

    Идея данного алгоритма состоит в нахождении сквозных путей с положительными потоками от источника к стоку.

    Рассмотрим ребро (i, j) с (начальной) пропускной способностью (C_ij,C_ji). В процессе выполнения алгоритма части этих пропускных способностей "забираются" потоками, проходящими через данное ребро, в результате каждое ребро будет иметь остаточную пропускную способность. Будем использовать запись (c_ij, c_ji) для представления остаточных пропускных способностей. Сеть, где все ребра имеют остаточную пропускную способность, назовем остаточной.

    Для произвольного узла j, получающего поток от узла i, определим метку [a_j, i], где a_j - величина потока, протекающего от узла i к узлу j. Алгоритм нахождения максимального потока предполагает выполнение следующих действий.

    Шаг 1. Для всех ребер (i, j) положим остаточную пропускную способность равной первоначальной пропускной способности, т.е. приравняем (c_ij, c_ji) = (C_ij, C_ji). Назначим a₁ = бесконечности и пометим узел 1 меткой [бесконечность, -]. Полагаем i = 1 и переходим ко второму шагу.

    Шаг 2. Определяем множество S_i как множество узлов j, в которые можно перейти из узла i по ребру с положительной остаточной пропускной способностью (т.е. c_ij > 0 для всех j, принадлежащих S_i). Если S_i не пустое множество, выполняем третий шаг, в противном случае переходим к шагу 4.

    Шаг 3. В множестве S_i находим узел k, такой, что c_ik = max {c_ij} для всех j, принадлежащих S_i. Положим a_k = c_ik и пометим узел k меткой [a_k, i]. Если последней меткой помечен узел стока (т.е. если k = n), сквозной путь найден, и мы переходим к пятому шагу.

    Шаг 4 (Откат назад). Если i = 1, сквозной путь невозможен, и мы переходим к шагу 6. Если i не равно 1, находим помеченный узел r, непосредственно предшествующий узлу i, и удаляем узел i из множества узлов, смежных с узлом r. Полагаем i = r и возвращаемся ко второму шагу.

    Шаг 5 (Определение остаточной сети). Обозначим через N_p = {1, k₁, k₂, …, n} множество узлов, через которые проходит p-й найденный сквозной путь от узла источника (узел 1) до узла стока (узел n). Тогда максимальный поток, проходящий по этому пути, вычисляется как f_p = min {a₁, a_k1, a_k2, ..., a_n}.

    Остальные пропускные способности ребер, составляющих сквозной путь, уменьшается на величину f_p в направлении движения потока и увеличиваются на эту же величину в противоположном направлении. Таким образом, для ребра (i, j), входящего в сквозной путь, текущие остаточные стоимости (c_ij, c_ji) изменятся следующим образом:

• (c_ij - f_p, c_ji + f_p), если поток идет от узла i к узлу j,
• (c_ij + f_p, c_ji - f_p), если поток идет от узла j к узлу i.

    Далее восстанавливаем все узлы, удаленные на шаге 4. полагаем i = 1 и возвращаемся ко второму шагу для поиска нового сквозного пути.

    Шаг 6 (Решение).

• При m найденных сквозных путях максимальный поток вычисляется по формуле F = f₁ + f₂ + ... + f_m.
• Имея значения начальных (C_ij, C_ji) и конечных (c_ij, c_ji) пропускных способностей ребра (i, j), можно вычислить оптимальный поток через это ребро следующим образом. Положим (a,b) = (C_ij - c_ij, C_ji - c_ji). Если a > 0, поток, проходящий через ребро (i, j), равен a. Если же b > 0, тогда поток равен b. (Случай, когда одновременно a > 0 и b > 0, невозможен.)

    Процесс отката назад на четвертом шаге выполняется тогда, когда алгоритм должен "убить" промежуточный узел до момента реализации сквозного пути. Коррекцию пропускных способностей, выполняемых на шаге 5, можно пояснить на примере простой сети, показанной на рис. 1. На рис. 1а найден первый сквозной путь N₁ = {1, 2, 3, 4} с максимальным потоком f₁ = 5. После этого остаточные пропускные способности ребер (1, 2), (2, 3) и (3, 4) изменятся соответственно с (5, 0) на (0, 5). На рис. 1б показан второй сквозной путь N₂ = {1, 3, 2, 4} с максимальным потоком f₂ = 5. После коррекции пропускных способностей получаем сеть, показанную на рис. 1в, где уже невозможно построить сквозной путь. Почему так получилось? При вычислении остаточных пропускных способностей на шаге 5 при переходе от сети (б) к сети (в) невозможна организация потока в направлении 2 -> 3. Получается, что алгоритм как бы "помнит", что поток в направлении 2 -> 3 уже был в предыдущих сквозных путях, и поэтому снова (на пятом шаге) изменяет пропускную способность с 0 до 5 в направлении от узла 3 к узлу 2.

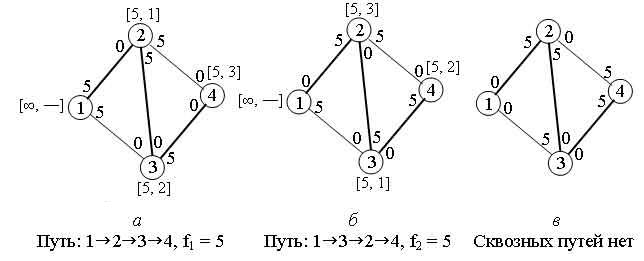
Рис.1. Иллюстрация сквозных путей

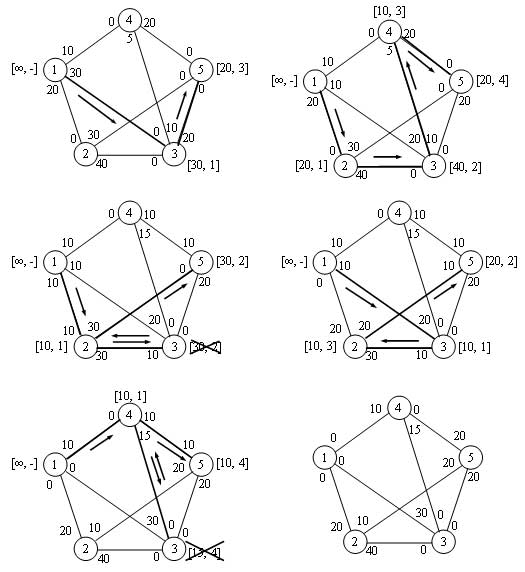
Рис.2. Графическая иллюстрация выполнения алгоритма

    Итерация 1.

    Положим остаточные пропускные способности (c_ij, c_ji) всех ребер равными первоначальным пропускным способностям (C_ij, C_ji).

    Шаг 1. Назначаем a₁ = бесконечности и помечаем узел 1 меткой [бесконечность,-]. Полагаем i = 1.

    Шаг 2. S₁ = [2, 3, 4] (множество не пустое).

    Шаг 3. k = 3, поскольку c₁₃ = max {c₁₂, c₁₃, c₁₄} = max {20, 30, 10} = 30. Назначаем a₃ = c₁₃ = 30 и помечаем узел 3 меткой [30, 1]. Полагаем i = 3 и возвращаемся к шагу 2.

    Шаг 2. S₂ = [4, 5].

    Шаг 3. k = 5 и a₅ = c₃₅ = max {10, 20} = 20. Помечаем узел 5 меткой [20,3]. Получен сквозной путь. Переходим к шагу 5.

    Шаг 5. Сквозной путь определяем по меткам, начиная с узла 5 и заканчивая узлом 1: (5) -> [20, 3] -> (3) -> [30, 1] -> (1). Таким образом, N₁ = {1, 3, 5} и f₁ = min {a₁, a₃, a₅} = {бесконечность, 30, 20} = 20. Вычисляем остаточные пропускные способности вдоль пути N₁:

  (c13, c31) = (30 - 20, 0 + 20) = (10, 20),
  (c35, c53) = (20 - 20, 0 + 20) = (0, 20).

    Итерация 2.

    Шаг 1. Назначаем a₁ = бесконечности и помечаем узел 1 меткой [бесконечность,-]. Полагаем i = 1.

    Шаг 2. S₁ = [2, 3, 4].

    Шаг 3. k = 2, назначаем a₂ = c₁₂ = max {20, 10, 10} = 20 и помечаем узел 2 меткой [20, 1]. Полагаем i =2 и возвращаемся к шагу 2.

    Шаг 2. S₃ = [4] (отметим, что c₃₅ = 0, поэтому узел 5 не включается в S₃).

    Шаг 3. k = 4, назначаем a₄ = c₃₄ = 10 и помечаем узел 4 меткой [10, 3]. Полагаем i = 4 и возвращаемся к шагу 2.

    Шаг 2. S₄ = [5] (поскольку узлы 1 и 3 уже помечены, они не включаются в S₄).

    Шаг 3. k = 5 и a₅ = c₄₅ = 20. Помечаем узел 5 меткой [20, 4]. Получаем сквозной путь. Переходим к шагу 5.

    Шаг 5. N₂ = {1, 2, 3, 4, 5} и f₂ = min {бесконечность, 20, 40, 10, 20} = 10. Вычисляем остаточные пропускные способности вдоль пути N₂:

  (c12, c21) = (20 - 10, 0 + 10) = (10, 10),
  (c23, c32) = (40 - 10, 0 + 10) = (30, 10),
  (c34, c43) = (10 - 10, 5 + 10) = (0, 15),
  (c45, c54) = (20 - 10, 0 + 10) = (10, 10).

    Итерация 3.

    Шаг 1. Назначаем a₁ = бесконечности и помечаем узел 1 меткой [бесконечность,-]. Полагаем i = 1.

    Шаг 2. S₁ = [2, 3, 4].

    Шаг 3. k = 2, назначаем a₂ = c₁₂ = max {10, 10, 10} = 10 и помечаем узел 2 меткой [10, 1]. Полагаем i = 2 и возвращаемся к шагу 2.

    Шаг 2. S₂ = [3, 5].

    Шаг 3. k = 3 и a₃ = c₂₃ = 30. Помечаем узел 3 меткой [30, 2]. Полагаем i = 3 и возвращаемся к шагу 2.

    Шаг 2. S₃ пусто, поскольку c₃₄ = c₃₅ = 0. Переходим к шагу 4.

    Шаг 4. Метка [30, 2] узла 3 показывает номер предшествующего узла r = 2. На этой итерации узел 3 в дальнейшем во внимание не принимается, его метку вычеркиваем. Полагаем i = r = 2 и возвращаемся к шагу 2.

    Шаг 2. S₄ = [5] (поскольку узел 3 удален из возможного сквозного пути).

    Шаг 3. k = 5 и a₅ = c₂₅ = 30. помечаем узел меткой [30, 2]. Получаем сквозной путь. Переходим к шагу 5.

    Шаг 5. N₃ = {1, 2, 5} и f₃ = min {бесконечность, 10, 30} = 10. Вычисляем остаточные пропускные способности вдоль пути N₃:

  (c12, c21) = (10 - 10, 10 + 10) = (0, 20),
  (c2, c52) = (30 - 10, 0 + 10) = (20, 10).

    Итерация 4. На этой итерации получен путь N₄ = {1, 3, 2, 5} с f₄ = 10.

    Итерация 5. На этой итерации получен путь N₅ = {1, 4, 5} с f₅ = 10.

    Итерация 6. Новые сквозные пути невозможны, поскольку все ребра, исходящие из узла 1, имеют нулевые остаточные пропускные способности. Переходим к шагу 6 для определения решения.

    Шаг 6. Максимальный объем потока в сети равен F = f₁ + f₂ + … +f₅ = 20 + 10 + 10 + 10 + 10 = 60 единиц. Значения потоков по различным ребрам вычисляются путем вычитания последних значений остаточных пропускных способностей (т.е. (c_ij, c_ji)₆) из первоначальных значений пропускных способностей (C_ij, C_ji). Результаты вычислений приведены ниже:

Ребро  (Cij, Cji)-(cij, cji)6        Величина потока  Направление
(1, 2)	(20, 0) - (0, 20) = (20, -20)	20	     1->2
(1, 3)	(30, 0) - (0, 30) = (30, -30)	30	     1->3
(1, 4)	(10, 0) - (0, 10) = (10, -10)	10	     1->4
(2, 3)	(40, 0) - (40, 0) = (0, 0)          0            -
(2, 5)	(30, 0) - (10, 20) = (20, -20)	20	     2->5
(3, 4)	(10, 5) - (0, 15) = (10, -10)	10	     3->4
(3, 5)	(20, 0) - (0, 20) = (20, -20)	20	     3->5
(4, 5)	(20, 0) - (0, 20) = (20, -20)	20	     4->5

    Приведем текст программы, решающей данную задачу:

#include <iostream.h>
#include <stdlib.h>  //Для функции abs().
#define TRUE 1
#define FALSE 0
#define MaxNodes 5   //Количество вершин.
#define MaxInt 1000  //Машинный эквивалент бесконечности.


//Описание типа узла.
struct Uzel
{
  int Element; //Заданный номер вершины.
  int Propusk; //Пропускная способность.
  int Metka;   //Помечена вершина или нет.
};


class Spisok
{
  private:
      int C[MaxNodes][MaxNodes];    //Матрица начальных пропускных способностей.
      int c[MaxNodes][MaxNodes];    //Матрица конечных пропускных способностей.
      int Put[MaxNodes][MaxNodes];  //Матрица сквозных путей.
      int Potok [MaxNodes];         //Потоки.
      int Est (Uzel*,int,int);
      int Tpk (int*,int,int);
  public:
      void Vvod_Ves();
      int Reshenie ();
      void Vyvod(int);

};

void main()
{
  Spisok A;

  A.Vvod_Ves();
  A.Vyvod(A.Reshenie());
}

void Spisok::Vvod_Ves()
//Ввод матрицы пропускных способностей.
{
  cout << "Вводите пропускные способности ребер:\n";
  for (int i=0;i<MaxNodes;i++)
   for (int j=0;j<MaxNodes;j++)
     {
       cout << "Введите C[" << (i+1) << "," << (j+1) << "]: "; 
       cin >> C[i][j];
       c[i][j] = C[i][j];
     }
}

void Spisok::Vyvod(int n)
//Вывод результатов.
{
  //Вычисление максимального объема потока.
  for (int i=0,sum=0;i<=n;sum+=Potok[i++]);
  cout << "\nМаксимальный объем потока в сети: " << sum;
  cout << "\nЗначения потоков по различным ребрам:\n";
  for (i=0;i<MaxNodes;i++)
   for (int j=i;j<MaxNodes;j++)
     if (C[i][j])
     {
         cout << "Ребро (" << (i+1) << "," << (j+1) <<"): ";
         cout << "(" << C[i][j]  << "," << C[j][i] << ")-(";
         cout << c[i][j]  << "," << c[j][i] << ")=(";
         cout << (C[i][j]-c[i][j]) << "," << (C[j][i]-c[j][i]) << ") ";
         cout << "Поток: " << abs(C[i][j]-c[i][j]) << " ";
         if (C[i][j]-c[i][j]!=0)
         {
           cout << "Направление: ";
           if (C[i][j]-c[i][j]>0)
              cout << (i+1) << "->" << (j+1);
           else
              cout << (j+1) << "->" << (i+1);
         }
         cout << endl;
     }
}

int Spisok::Reshenie()
{
  Uzel SS[MaxNodes]; //Множество узлов, в которые можно перейти.
  Uzel S[MaxNodes]; //Путь.
  int i,j=0,k,el,mx,mn;
  int m; //Текущее количество вершин в пути.
  int nomer=-1; //Текущее количество сквозных потоков.
  int Tupik[MaxNodes]; //Перечень "тупиковых" вершин.
  int N_Tupik; //Количество элементов в массиве.

  while (j!=-1)
  {
    i=m=0;
    S[i].Element=0;
    S[i].Propusk=MaxInt;
    S[i].Metka=TRUE;
    el=0;
    N_Tupik=-1;
    while (el!=MaxNodes-1)
    {
      j=-1;
      for (k=0;k<MaxNodes;k++)
       if (c[i][k]!=0) //Если есть ненулевой поток...
        if (i>0)   //и в путь уже включены вершины...
        {
          if (!Est(&S[0],m,k) && !Tpk(&Tupik[0],N_Tupik,k)) 
                            //то включаем текущую вершину,
                           //если ее нет в пути и если она не "тупиковая".
          {  
             SS[++j].Element=k;
             SS[j].Propusk=c[i][k];
             SS[j].Metka=FALSE;
          }
        }
        else 
          if (!Tpk(&Tupik[0],N_Tupik,k)) //Не вернулись ли назад?
               //Поток не нулевой, и это первая вершина.
          {    //Включаем эту вершину в путь.
               SS[++j].Element=k;
               SS[j].Propusk=c[i][k];
               SS[j].Metka=FALSE;
          }
      if (j!=-1) //Есть продолжение.
      {
         mx=SS[0].Propusk;
         el=0;
         for (k=1;k<=j;k++)
          if (SS[k].Propusk>mx)
            { el=k; mx=SS[k].Propusk; }
         S[++m].Element=SS[el].Element;
         S[m].Propusk=mx;
         S[m].Metka=TRUE;
         if (SS[el].Element==MaxNodes-1) //Найден сквозной путь.
         {
           nomer++;
           //Запоминаем сквозной путь.
           for (k=0;k<=m;k++)
              Put[nomer][k]=S[k].Element;
           //Ищем минимальный поток.
           mn=S[0].Propusk;
           el=0;
           for (k=1;k<=m;k++)
            if (S[k].Propusk<mn)
              { el=k; mn=S[k].Propusk; }
           Potok[nomer]=mn; //Запоминаем его.
           //Вычисляем остаточные пропускные способности.
           for (k=0;k<m;k++)
           { 
             c[S[k].Element][S[k+1].Element] -= Potok[nomer];
             c[S[k+1].Element][S[k].Element] += Potok[nomer];
           }
           el=MaxNodes-1; //Переход к следующей итерации.
           j=0;
         }
         else i=S[m].Element;
      }
      else //Продолжения нет. Это возможно тогда, когда:
      {
         if (i==0)  //а) все пропускные способности нулевые.
                    //   В этом случае - выход
              el=MaxNodes-1;
         else       //б) мы попали в тупик. Запомним тупиковую вершину
                    //   в массиве и отступим назад на одну вершину.
         {
           Tupik[++N_Tupik]=S[m].Element;
           m--;
           i=S[m].Element;
         }
      }
    }
  }
  return nomer; //Возвращает количество сквозных потоков.
}

int Spisok::Est(Uzel S[], int m, int k)
//Функция проверяет, есть ли вершина k в пути S.
//m - текущее количество элементов в пути.
//Возвращает 1, если вершина есть, и 0 - в противном случае.
{
  for (int l=0;l<=m;l++)
    if (S[l].Element==k) return 1;
  return 0;
}

int Spisok::Tpk(int Tupik[],int N_Tupik, int k) 
//Функция проверяет, есть ли вершина k в массиве "тупиковых" вершин.
//N_Tupik - текущее количество вершин в массиве.
//Возвращает 1, если вершина есть, и 0 - в противном случае.
{
  if (N_Tupik==-1) return 0;
  for (int l=0;l<=N_Tupik;l++)
    if (Tupik[l]==k) return 1;
  return 0;
}

    Результат работы этой программы для сети, изображенной на рисунке 2, будет следующим:

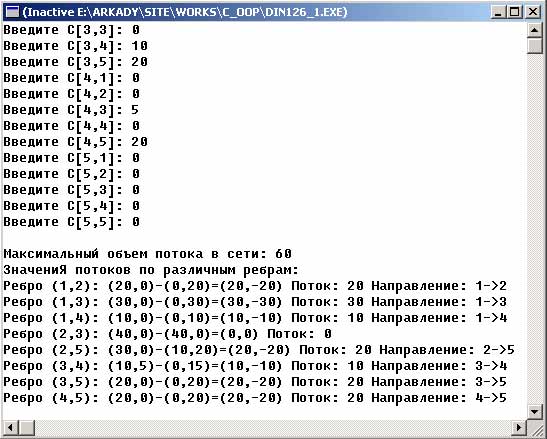
Рис.3. Результат работы приложения

    Со следующего шага мы начнем рассматривать задачу о нахождении потока наименьшей стоимости.

Предыдущий шаг Содержание Следующий шаг