На этом шаге мы сформулируем задачу о максимальном потоке.
Рассмотрим сеть трубопроводов для транспортировки сырой нефти от буровых скважин до нефтеперегонных заводов. Для перекачки нефти предусмотрены магистральные насосные станции. Каждый сегмент трубопровода имеет свою пропускную способность. Сегменты трубопровода могут быть как однонаправленные (осуществляют перекачку нефти только в одном направлении), так и в двунаправленные. В однонаправленных сегментах положительная пропускная способность предполагается в одном направлении и нулевая - в другом. На рис. 1 показана типовая сеть нефтепроводов. Как определить оптимальную пропускную способность (т.е. максимальный поток) между нефтяными скважинами и нефтеперегонными заводами?
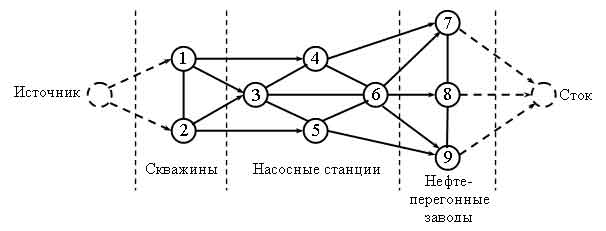
Рис.1. Типовая сеть нефтепроводов
При решении данной задачи исходную сеть необходимо свести к сети с одним источником и одним стоком. Этого можно достигнуть путем введения дополнительных дуг с бесконечной пропускной способностью от источника к скважинам и от нефтеперегонных заводов к стоку (на рис. 1 эти дуги показаны пунктирными линиями).
Для ребра (i, j), где i < j, используем запись (Cij,Cji) для представления пропускных способностей в направлениях i->j и j->i соответственно. Во избежании недоразумений на схеме сети Cij будем располагать на ребре (i, j) ближе к узлу i, а Cji ближе к узлу j, как показано на рис. 2.

Рис.2. Иллюстрация пропускной способности
Перебор разрезов
Разрез определяет множество ребер, при удалении которых из сети полностью прекращается поток от источника к столу. Пропускная способность разреза равна сумме пропускных способностей "разрезанных" ребер. Среди всех разрезов сети разрез с минимальной пропускной способностью определяет максимальный поток в сети.
Пример. Рассмотрим сеть, показанную на рис. 3. На этом рисунке при обозначении пропускных способностей двунаправленных ребер придерживались соглашения, принятого ранее (рис. 2). Например, для ребра (3, 4) пропускная способность в направлении 3 -> 4 равна 10, а в направлении 4 -> 3 равна 5.
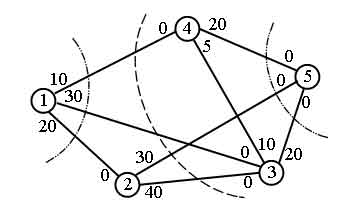
Рис.3. Пример сети
Разрезы, представленные на рис. 3, имеют следующие пропускные способности:
Разрез "Разрезанные" ребра Пропускная способность 1 (1, 2), (1, 3), (1, 4) 10 + 30 + 20 = 60 2 (1, 3), (1, 4), (2, 3), (2, 5) 30 + 10 + 40 + 30 = 110 3 (2, 5), (3, 5), (4, 5) 30 + 20 + 20 = 70
Вывод, который можно сделать из этих трех разрезов, заключается в том, что максимальный поток не может превышать 60 единиц. Но мы не можем сказать, какой максимальный поток на самом деле, так как не перебрали все возможные разрезы сети. К сожалению, перебор всех разрезов является непростой задачей. Поэтому для определения максимального потока в сети не используются алгоритмы, основанные на полном переборе разрезов.
На следующем шаге мы рассмотрим алгоритм нахождения максимального потока.
