На этом шаге мы рассмотрим преобразование сетевой модели в задачу линейного программирования.

Определение модели сети с ограниченной пропускной способностью как задачи линейного программирования необходимо для разработки симплексного алгоритма решения задач данного типа. Используя определения, данные в шаге 127, мы можем записать задачу линейного программирования для сети с ограниченной пропускной способностью следующим образом.

Минимизировать:

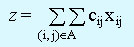
при ограничениях:

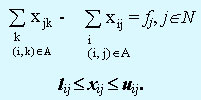
Результирующий "чистый" поток f_j, протекающий через узел j, вычисляется по формуле

    f_j = (Величина потока, выходящего из узла j) - 
                      (Величина потока, входящего в узел j).

Узел j выступает в качестве источника, если f_j > 0, и как исток при f_j < 0.

Нижнюю границу пропускной способности l_ij можно удалить из ограничений с помощью подстановки x_ij = x'_ij - l_ij. Для нового потока верхней границей пропускной способности будет величина u_ij - l_ij. В этом случае результирующий поток через узел i будет равен [f_i] - l_ij, а через узел j - [f_j] + l_ij. На рисунке 1 показаны преобразования характеристик дуги (i, j) после исключения ее нижней границы пропускной способности.

Рис.1. Преобразования характеристик

Пример 1. Запишем задачи линейного программирования для сети из рисунка 2 до и после исключения нижних границ пропускных способностей.

Основные ограничения формулируемой задачи линейного программирования связаны с определением входных и выходных потоков, протекающих через каждый узел, что порождает следующую задачу линейного программирования:

              x₁₂    x₁₃    x₁₄    x₂₃    x₂₅    x₃₄    x₃₅    x₄₆    x₅₆
Миними-       3      4      1      5      6      1      2      2      4	
зировать
Узел 1        1      1      1                                               = 100
Узел 2       -1                    1      1                                 = 200
Узел 3              -1            -1             1      1                   =  50
Узел 4                     -1                   -1             1            =-150
Узел 5                                   -1            -1             1     = -80
Узел 6                                                        -1     -1     =-120
Нижние        0      0     50      0      0     70      0    100      0	
границы										
Верхние       Б      Б     80      Б      Б    120      Б    120      Б 	
границы										

Примечание. Б - бесконечность.

Сделаем замечание о структуре коэффициентов, формирующих ограничения. В столбце, соответствующем переменной x_ij, всегда в строке i стоит +1, а в строке j находится -1. Остальные коэффициенты равны нулю. Такая структура коэффициентов типична для сетевых моделей.

Для переменных, представляющих потоки через дуги, имеющие ненулевые нижние границы пропускных способностей, выполняем замену:

  x₁₄ = x'₁₄ + 50,
  x₃₄ = x'₃₄ + 70,
  x₄₆ = x'₄₆ + 100.

В результате получаем следующую задачу линейного программирования:

              x₁₂    x₁₃    x₁₄    x₂₃    x₂₅    x₃₄    x₃₅    x₄₆    x₅₆
Миними-       3      4      1      5      6      1      2      2      4	
зировать
Узел 1        1      1      1                                               =  50
Узел 2       -1                    1      1                                 = 200
Узел 3              -1            -1             1      1                   = -20
Узел 4                     -1                   -1             1            =-130
Узел 5                                   -1            -1             1     = -80
Узел 6                                                        -1     -1     = -20
Верхние       Б      Б     30      Б      Б     50      Б     20      Б 	
границы										

Примечание. Б - бесконечность.

Соответствующая сеть после исключения нижних границ пропускных способностей дуг показана на рисунке 2.

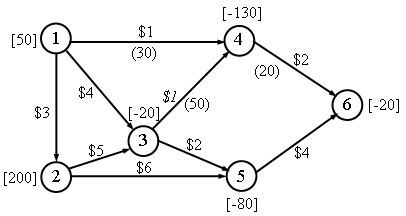
Рис.2. Сеть после исключения нижних границ

Отметим, что данную сеть можно получить непосредственно из сети, представленной на рисунке 3, с помощью преобразований, показанных на рисунке 1, причем без необходимости записи в виде задачи линейного программирования.

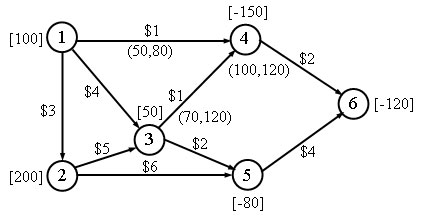
Рис.3. Схема маршрутов

В следующем примере представлена сетевая модель, которая исходно не удовлетворяет условию узлового потока (т.е. условию, что результирующий поток, проходящий через узел, равен разности выходного и входного потоков), но которую можно преобразовать в модель, удовлетворяющую этому условию, путем изменения ограничений соответствующей задачи линейного программирования.

Пример 2. Агентство по найму рабочей силы имеет заказ на рабочих на 4 месяца вперед (с января по апрель) согласно следующему графику:

    Месяц             Январь   Февраль   Март     Апрель
К-во рабочих           100       120      80       170

Поскольку спрос на рабочих различен в разные месяцы, возможно, экономически целесообразно нанять больше рабочих, чем требуется, в текущем месяце. Стоимость найма рабочих и удержания их в "ждущем режиме" зависит от времени трудоустройства, как показано в следующей таблице:

Время трудоустройства (месяцы)           1    2    3    4
Стоимость на одного рабочего (рубли)    100  130  180  220

Обозначим через x_ij количество рабочих, нанятых на начало i-го месяца и освобожденных на начало j-го. Например, x₁₂ - это количество рабочих, нанятых в январе только на один месяц.

Чтобы сформулировать задачу линейного программирования, нужно добавить еще пятый месяц (май). Тогда, например, переменная x₄₅ будет обозначать количество рабочих, нанятых в апреле на один месяц. Естественно, на май нет заказа на рабочих.

Ограничения строятся так, чтобы спрос на рабочих в месяц k можно было бы удовлетворить за счет всех рабочих xij, где i<=k<=j. Обозначив через S_i (S_i>=0) количество рабочих, "лишних" в месяце i, получим следующую задачу линейного программирования:

      x₁₂  x₁₃  x₁₄  x₁₅  x₂₃  x₂₄  x₂₅  x₃₄  x₃₅  x₄₅  S₁  S₂  S₃  S₄	
      100  130  180 220  100  130 180  100  130  100                  Min
Янв.   1    1    1   1                                -1              100
Фев.        1    1   1    1    1   1                      -1          120
Март             1   1         1   1    1    1                -1       80
Апр.                 1             1         1    1              -1   170

В данной задаче линейного программирования нет той специальной структуры коэффициентов ограничений, что была в модели из примера 1. Тем не менее, эта задача имеет свою специфику, которая позволит преобразовать ее в сетевую модель. Выполним следующие действия.

Из n-го уравнения (ограничения) задачи создадим новое (n + 1)-е уравнение, умножив n-е уравнение на -1.
Оставляем первое уравнение без изменений.
Для i = 2, 3, …, n последовательно заменяем i-е уравнение разностью i-го и (i - 1)-го уравнений.

Применение описанной процедуры к задаче данного примера приводит к следующей задаче линейного программирования, которая уже имеет структуру сетевой модели.

Таким образом, задачу распределения рабочих можно представить в виде эквивалентной задачи нахождения потока минимальной стоимости в сети с ограниченной пропускной способностью (рисунок 4):

      x₁₂  x₁₃  x₁₄  x₁₅  x₂₃  x₂₄  x₂₅  x₃₄  x₃₅  x₄₅  S₁  S₂  S₃  S₄	
      100  130  180 220  100  130 180  100  130  100                   Min
Янв.   1    1    1   1                                -1               100
Фев.  -1                  1    1   1                   1  -1            20
Март       -1            -1             1    1             1  -1       -40
Апр.            -1            -1       -1         1            1 -1     90
Май                 -1            -1   -1   -1   -1              -1   -170

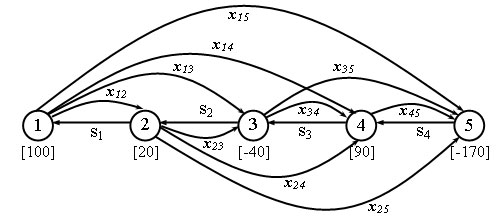
Рис.4. Сеть с ограниченной пропускной способностью

Задачу линейного программирования можно решить с помощью специализированных программных средств, например Microsoft Excel.

На следующем шаге мы рассмотрим симплексный алгоритм для сетей с ограниченной пропускной способностью.

Предыдущий шаг Содержание Следующий шаг