На этом шаге мы приведем пример использования симплексного метода при решении сетевых задач.

    Предлагаемый алгоритм повторяет в точности те же шаги, что и обычный симплексный метод. Вместе с тем здесь учитывается специальная структура сетевой модели.

    Используя определения из предыдущего шага, f_i - результирующий поток через узел i, строим симплексный алгоритм на основе условия равенства нулю суммы f_i при i, изменяющимся от 1 до n. Это условие означает, что в сети суммарный объем предложений равен суммарному объему спроса. Мы всегда можем удовлетворить данное условие путем введения фиктивного источника или стока, которые можно связать с остальными узлами сети дугами с нулевой стоимостью и бесконечной пропускной способностью. Однако сбалансированность сети не гарантирует существования допустимого решения, поскольку этому может воспрепятствовать ограниченность пропускных способностей дуг.

    Опишем шаги алгоритма нахождения потока минимальной стоимости для сетей с ограниченной пропускной способностью.

    Шаг 0. Определяем для данной сети начальное базисное допустимое решение (множество дуг). Переходим к шагу 1.

    Шаг 1. С помощью условия оптимальности симплекс-метода определяем вводимую в базис переменную (дугу). Если на основе условия оптимальности определяем, что последнее решение оптимально, вычисления заканчиваются. В противном случае переходим к шагу 2.

    Шаг 2. На основе условия допустимости симплекс-метода определяем исключаемую из базиса переменную (дугу). Изменив базис, возвращаемся к шагу 1.

    Сети с n узлами и нулевым результирующим потоком (т.е. при выполнении равенства f₁ + f₂ +…+ f_n = 0) соответствуют n - 1 независимым ограничениям в виде равенств. Поэтому базисное решение должно содержать n - 1 переменных. Можно показать, что базисное решение соответствует остовному дереву данной сети.

    Вводимая переменная (дуга) на шаге 1 определяется путем вычисления разностей z_ij - c_ij для всех текущих небазисных дуг (i, j). Если для всех разностей z_ij - c_ij <= 0, тогда текущее базисное решение оптимально. Иначе в качестве вводимой в базис переменной выбираем дугу, которой соответствует наибольшее положительное значение разности z_ij - c_ij.

    Вычисление разностей z_ij - c_ij основано на соотношениях двойственности, точно так же как в транспортной модели. Обозначим через w_i переменную задачи, двойственной к задаче линейного программирования, которая (переменная) соответствует ограничению узла i. Тогда данная двойственная задача формулируется следующим образом.

    Максимизировать

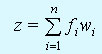
при выполнении условий

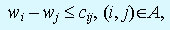
переменные w_i произвольного знака (i = 1, 2, …, n).

    Из теории линейного программирования следует, что w_i - w_j = c_ij для любой базисной дуги (i, j). Поскольку исходная задача линейного программирования по определению имеет одно избыточное ограничение, мы можем присвоить произвольное значение одной из переменной двойственной задачи. Для определенности положим w₁ = 0. Затем следует решить (базисную) систему уравнений w_i - w_j = c_ij для нахождения остальных переменных двойственной задачи. Далее вычисляем разности z_ij - c_ij для небазисных переменных согласно формуле

    zij - cij = wi - wj - сij.

    Теперь осталось показать, как определяется исключаемая из базиса переменная. Для этого рассмотрим следующий числовой пример.

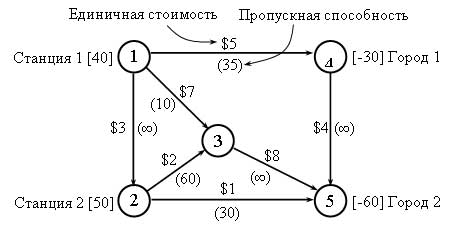
Рис.1. Пример сети

    Итерация 0.

    Шаг 0. Определение начального допустимого базисного решения. Нетрудно построить остовное дерево (на рис. 2 показано сплошными дугами) для рассматриваемой сети. Отсюда получаем начальное допустимое базисное решение. Обычно для нахождения такого решения используется метод введения искусственных переменных.

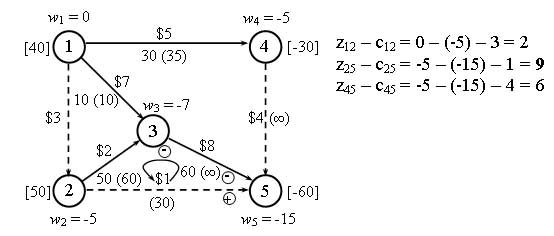
Рис.2. Остовное дерево

    На рис. 2 показано, что базисному решению соответствуют дуги (1, 3), (1,4) и (3, 5) с потоками 30, 10, 50 и 60 единиц соответственно. Оставшиеся дуги (показаны пунктиром) представляют небазисные переменные. Запись x(c) показывает, что через соответствующую дугу с пропускной способностью c проходит поток x.

    Итерация 1.

    Шаг 1. Определение вводимой в базис переменной. При решении системы уравнений

    w1 = 0,
    wi - wj = cij для базисных дуг (i, j)

    Дуга (1, 3): w1 - w3 = 7 ==> w3 = -7.
    Дуга (1, 4): w1 - w4 = 5 ==> w4 = -5.
    Дуга (2, 3): w2 - w3 = 2 ==> w2 = -5.
    Дуга (3, 5): w3 - w5 = 8 ==> w5 = -15.

    Теперь вычисляем разности z_ij - c_ij для небазисных переменных.

    Дуга (1, 2): w1 - w2 - c12 = 0 - (-5) - 3 = 2.
    Дуга (2, 5): w2 - w5 - c25 = (-5) - (-15) - 1 = 9.
    Дуга (4, 5): w4 - w5 - c45 = (-5) - (-15) - 4 = 6.

    Таким образом, дуга (2, 5) будет введена в базисное решение.

    Шаг 2. Определение исключаемой из базиса переменной. На рис. 2 видно, что дуга (2, 5) совместно с базисными дугами (2, 3) и (3, 5) образуют цикл. По определению остовное дерево не может содержать циклов. Поскольку поток через дугу (2, 5) должен возрасти, необходимо выровнять потоки через дуги, составляющие цикл таким образом, чтобы новое решение осталось допустимым. Для этого поток через дугу (2, 5) пометим знаком "+", потоки через другие дуги цикла - знаком "+" или "-", в зависимости от того, будут ли совпадать направления потоков в этих дугах с направлением потока в дуге (2, 5) при обходе цикла против часовой стрелки. Пометки дуг цикла показаны на рис. 2.

    При определении максимального потока, протекающего через дугу (2, 5), необходимо придерживаться следующих правил.

1. Новый поток в текущей базисной дуге не может быть отрицательным.
2. Поток через вводимую в базис дугу не может превышать ее пропускную способность.

    Применение правила 1 показывает, что потоки через дуги (2, 3) и (3, 5) нельзя уменьшить более, чем на min {50, 60} = 50 единиц. Из правила 2 следует, что поток через дугу (2, 5) не может превышать 30 единиц (пропускная способность этой дуги равна 30). Поэтому поток через дуги цикла изменится не более, чем на min {30, 50} = 30 единиц. Таким образом, поток через дугу (2, 5) равен 30 единицам, через дугу (2, 3) - 50 - 30 = 20 единицам, а через дугу (3, 5) - 60 - 30 =30 единицам.

    Поскольку никакая из текущих базисных переменных не приняла нулевого значения, дуга (2, 5) должна остаться небазисной, но с ненулевым значением в 30 единиц. Чтобы выполнить требование равенства нулю небазисных переменных, сделаем подстановку

    x25 = 30 - x52, 0 <= x52 <=  30.

    Эта подстановка изменит уравнения для потоков, протекающих через узлы 2 и 5.

    Текущее уравнение для потоков узла 2: 50 + x12 = x23 + x25.
    Текущее уравнение для потоков узла 5: x25 + x35 + x45 = 60.

    Новое уравнение для потоков узла 2: 20 + x12 + x52 = x23.
    Новое уравнение для потоков узла 5:  x35 + x45 = x52 + 30.

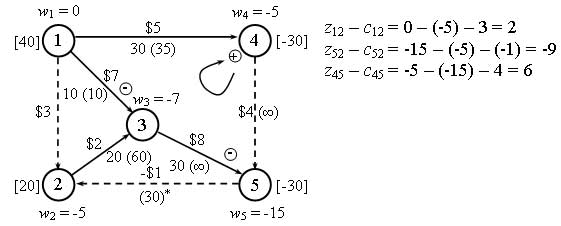
Рис.3. Результаты изменения сети

    Итерация 2.

    На рисунке 3 представлены новые значения разностей z_ij - c_ij. Очевидно, что в базис следует ввести дугу (4, 5). Введение в базис этой дуги также приводит к образованию цикла.

    Величину потока через дугу (4, 5) можно увеличить до наименьшей из следующих величин.

1. Максимальный поток через дугу (4, 5), определяемый пропускной способностью, равен бесконечности.
2. Максимальное увеличение потока через дугу (1, 4) равно 35 - 30 = 5 единиц.
3. Максимальное уменьшение потока через дугу (1, 3) равно 10 единиц.
4. Максимальное уменьшение потока через дугу (3, 5) равно 30 единиц.

    Таким образом, поток через дугу (4, 5) можно увеличить до 5 единиц; эта дуга входит в базис, а дуга (1, 4) с потоком в 35 единиц исключается из базиса.

    Выполнив подстановку x₁₄ = 35 - x₄₁, получим сеть, показанную на рис. 4, где дуги (1, 3), (2, 3), (3, 5) и (4, 5) формируют остовное дерево сети (базисное решение). Для дуги (1, 4) с обратным направлением потока изменена стоимость прохождения потока до -$5.

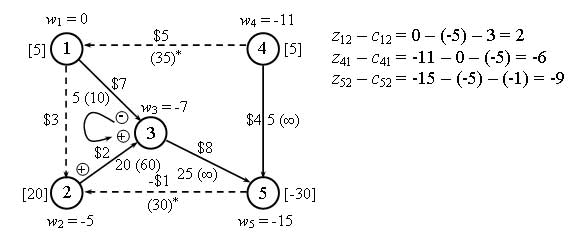
Рис.4. Результирующая сеть

    Итерация 3.

    Вычисленные новые значения разностей z_ij - c_ij для небазисных дуг (1, 2), (4, 1) и (5, 2) показаны на рис. 4. Из этих значений вытекает, что в базис следует ввести дугу (1, 2) с потоком в 5 единиц, тогда как дуга (1, 3) исключается из базиса с нулевым значением потока. Новое решение представлено на рисунке 5.

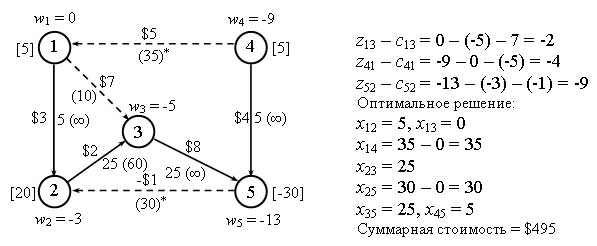
Рис.5. Новое решение

    Итерация 4.

    Из новых значений разностей z_ij - c_ij (рис. 5) видно, что последнее решение оптимально. Значения исходных переменных получаем путем обратной подстановки, как показано на рисунке 5.

    Со следующего шага мы начнем знакомиться с методами сетевого планирования.

Предыдущий шаг Содержание Следующий шаг