На этом шаге мы рассмотрим алгоритм определения критического пути.

    Конечным результатом применения метода критического пути будет построение временного графика выполнения проекта (см. рис. 1 шага 131). Для этого проводятся специальные вычисления, в результате чего получаем следующую информацию.

1. Общая длительность выполнения проекта.
2. Разделение множества процессов, составляющих проект, на критически и некритические.

    Процесс является критическим, если он не имеет "зазора" для времени своего начала и завершения. Таким образом, чтобы весь проект завершился без задержек, необходимо, чтобы все критические процессы начинались и заканчивались в строго определенное время. Для некритического процесса возможен некоторый "дрейф" времени его начала, но в определенных границах, когда время его начала не влияет на длительность выполнения всего проекта.

    Для проведения необходимых вычислений определим событие как точку на временной оси, где завершается один процесс и начинается другой. В терминах сети, событие - это сетевой узел. Нам понадобятся также следующие определения и обозначения:

• A_j - самое раннее возможное время наступления события j,
• B_j - самое позднее возможное время наступления события j,
• D_ij - длительность процесса (i, j).

    Вычисления критического пути включает два этапа (прохода). При проходе вперед вычисляются самые ранние времена наступления событий, а при проходе назад - самые поздние времена наступления тех же событий.

    Проход вперед. Здесь вычисления начинаются в узле 1 и заканчиваются в последнем узле n.

    Начальный шаг. Полагаем A₁=0; это указывает на то, что проект начинается в нулевой момент времени. Основной шаг j. Для узла j определяем узлы p, q, …, v, непосредственно связанные с узлом j процессами (p, j), (q, j), …, (v, j), для которых уже вычислены самые ранние времена наступления соответствующих событий. Самое раннее время наступления события j вычисляется по формуле

    Aj = max { Ap + Dpj,  Aq + Dqj, …,  Av + Dvj}.

    Проход вперед завершается, когда будет вычислена величина A_n для узла n. По определению величина j равна самому длинному пути (длительности) от начала проекта до узла (события) j.

    Проход назад. В этом проходе вычисления начинаются в последнем узле n и заканчивается в узле 1.

    Начальный шаг. Полагаем B_n = A_n; это указывает, что самое раннее и самое позднее времена для завершения проекта совпадают.

    Основной шаг j. Для узла j определяем узлы p, q, …, v, непосредственно связанные с узлом j процессами (j, p), (j, q), …, (j, v), для которых уже вычислены самые поздние времена наступления соответствующих событий. Самое позднее время наступления события j вычисляется по формуле

    Bj = min {Bp - Djp, Bq - Djq, …, Bv - Djv}.

    Проход назад завершается при вычислении величины B₁ для узла 1.

    Процесс (i, j) будет критическим, если выполняются три условия.

1. B_i = A_i.
2. B_j = A_j.
3. B_j - B_i = A_j - A_i = D_ij.

    Эти условия не выполняются, то процесс некритический.

    Критические процессы должны образовывать непрерывный путь через всю сеть от начального события до конечного.

    Проход вперед.

    Узел 1. Полагаем A₁ = 0.

    Узел 2. A₂ = A₁ + D₁₂ = 0 + 5 = 5.

    Узел 3. A₃ = max { A₁ + D₁₃, A₂ + D₂₃} = max {0 + 6, 5 + 3} = 8.

    Узел 4. A₄ = A₂ + D₂₄ = 5 + 8 = 13.

    Узел 5. A₅ = max { A₃ + D₃₅, A₄ + D₄₅} = max {8 + 2, 13 + 0} = 13.

    Узел 6. A₆ = max { A₃ + D₃₆, A₄ + D₄₆, A₅ + D₅₆} = max {8 + 11, 13 + 1, 13 + 12} = 25.

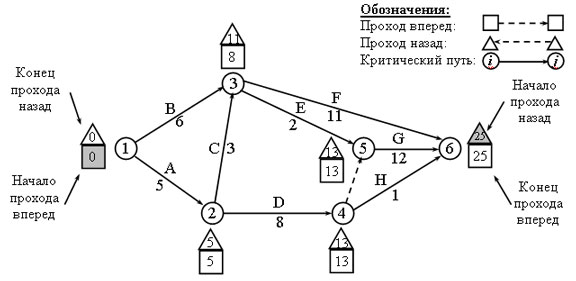
Рис.1. Пример проекта

    Таким образом, расчеты показывают, что проект можно выполнить за 25 дней.

    Проход назад.

    Узел 6. Полагаем A₆ = B₆ = 25.

    Узел 5. B₅ = B₆ - D₅₆ = 25 - 12 = 13.

    Узел 4. B₄ = min {B₆ - D₄₆, B₅ - D₄₅} = min {25 - 1, 13 - 0} = 13.

    Узел 3. B₃ = min {B₆ - D₃₆, B₅ - D₃₅} = min {25 - 11, 13 - 2} = 11.

    Узел 2. B₂ = min {B₄ - D₂₄, B₃ - D₂₃} = min {13 - 8, 11 - 3} = 5.

    Узел 1. B₁ = min {B₃ - D₁₃, B₂ - D₁₂} = min {11 - 6, 5 - 5} = 0.

    Вычисления без ошибок всегда приводят к результату B = 0.

    Результаты вычислений, выполняемых при проходах вперед и назад, показаны на рисунке 1. Правила определения критических процессов показывают, что критический путь составляют процессы 1->2->4->5->6, т.е. этот путь проходит от начального узла 1 до конечного узла 6. Сумма длительности критических процессов (1, 2), (2, 4), (4, 5) и (5, 6) равна длительности всего проекта (т.е. 25 дней). Отметим, что процесс (4, 6) удовлетворяет первым двум условиям критического пути (B₄ = A₄ = 13 и B₆ = A₆ = 25), но не удовлетворяет третьему условию ( A₆ - B₄ не равно D₄₆). Поэтому данный процесс не является критическим.

    Для проверки полученных результатов воспользуемся программой, приведенной на 121 шаге, которая позволяет спланировать критический путь. Для заданных исходных данных результат вычислений по этой программе будет следующим:

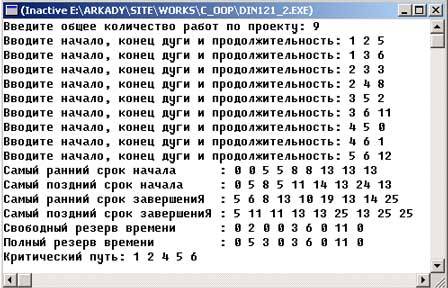
Рис.2. Результат работы приложения

    На следующем шаге мы рассмотрим построение временного графика.

Предыдущий шаг Содержание Следующий шаг