На этом шаге мы рассмотрим некоторые преобразования координат.

Сначала рассмотрим общие вопросы преобразования координат. Пусть задана n-мерная система координат в базисе (k₁, k₂,.... k_n), описывающая положение точки в пространстве с помощью числовых значений k_i. В компьютерной графике чаще всего используется двумерная (n=2) и трехмерная (n=3) системы координат.

Если задать другую, N-мерную, систему координат в базисе (m₁, m₂,..., m_N) и поставить задачу определения координат в новой системе, зная координаты в старой, то решение (если оно существует) можно записать в таком виде:

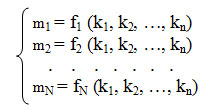
где f_i - функция пересчета i-й координаты, аргументы - координаты в системе k_i.

Можно поставить и обратную задачу - по известным координатам m₁, m₂,..., m_N определить координаты k₁, k₂,.... k_n. Решение обратной задачи запишем так:

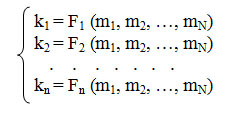
где F_i - функции обратного преобразования.

В случае, когда размерности систем координат не совпадают (n <> N), осуществить однозначное преобразование координат зачастую не удается. Например, по двумерным экранным координатам нельзя без дополнительных условий однозначно определить трехмерные координаты отображаемых объектов.

Если размерности систем совпадают (n = N), то также возможны случаи, когда нельзя однозначно решить прямую или обратную задачи.

Преобразование координат классифицируют:

по системам координат - например, преобразование из полярной системы в прямоугольную;
по виду функций преобразования f_i.

По виду функций преобразования различают линейные и нелинейные преобразования. Если при всех i = 1, 2, ... , N функции f_i - линейные относительно аргументов (k₁, k₂,.... k_n), то есть

  f_i = a_i1k₁+ a_i2k₂+ ... + a_ink_n+ a_i,n+1

где a_i,j - константы, то такие преобразования называются линейными, а при n = N - аффинными.

Если хотя бы для одного i функция f - нелинейная относительно (k₁, k₂,.... k_n), тогда преобразование координат в целом не линейно.

Например, преобразование

  X = 3х + 5y,
  Y = 4xy + 10y

нелинейное, так как в выражении для Y присутствует xy.

Линейные преобразования наглядно записываются в матричной форме:

Здесь матрица коэффициентов (а_ij) умножается на матрицу-столбец (k_i) и в результате получается матрица-столбец (m_i).

Напомним некоторые факты из алгебры матриц. Для двух матриц А размером (m*n) и В размером (n*p):

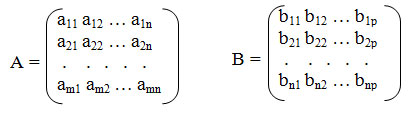
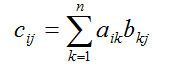
произведением матриц является матрица С = А*В размером (m*p):

для которой элементы c_ij вычисляются по формуле:

Правило вычисления элементов матрицы С можно легко запомнить по названию "строка на столбец". И действительно, для вычисления любого элемента c_ij необходимо умножить элементы i-й строки матрицы А на элементы j-го столбца матрицы В.

Произведение матриц определено только для случая, когда количество столбцов матрицы А равно количеству строк матрицы В.

Вернемся к преобразованиям координат. Рассмотрим более подробно некоторые отдельные типы преобразований.

На следующем шаге мы рассмотрим аффинные преобразования на плоскости.

Предыдущий шаг Содержание Следующий шаг