На этом шаге мы рассмотрим аффинные преобразования на плоскости.

Зададим некоторую двумерную систему координат (х, у). Аффинное преобразование координат (х, у) описывается формулами

  X = Ах + By + С,
  Y = Dx + Ey + F,

где А, В, ..., F - константы. Значения (X, Y) можно трактовать как координаты в новой системе координат.

Обратное преобразование (X, Y) в (х, у) также является аффинным:

  х = А'Х'+ B'Y+ С', 
  у = D'X + Е'Y + F'.

Аффинное преобразование удобно записывать в матричном виде. Константы А, В, ...., F образовывают матрицу преобразования, которая, будучи умноженная на матрицу-столбец координат (х, у), дает матрицу-столбец (X, Y). Однако для того, чтобы учесть константы С и F, необходимо перейти к так называемым однородным координатам - добавим строку с единицами в матрицах координат:

Матричная запись дает возможность наглядно описывать несколько преобразований, которые идут одно за другим. Например, если необходимо сначала выполнить преобразования:

а потом - другое преобразование:

то это можно описать как:

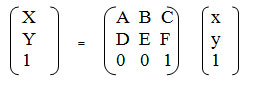
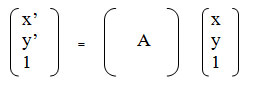
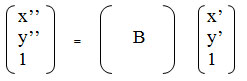
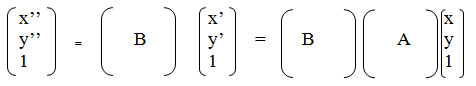
Однако вместо двух преобразований можно выполнить только одно:

где матрица (С) равна произведению (В)(А).

Перемножение матриц выполняется так, как это принято в линейной алгебре.

Рассмотрим частные случаи аффинного преобразования.

1. Параллельный сдвиг координат (рисунок 1).

В матричной форме:

Рис.1. Параллельный сдвиг координат

Обратное преобразование:

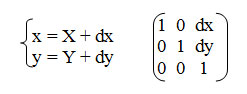
2. Растяжение-сжатие осей координат (рисунок 2).

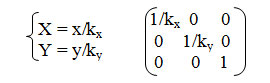
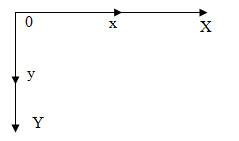
Рис.2. Растяжение/сжатие осей координат

Обратное преобразование:

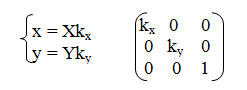
Коэффициенты k_x и k_y могут быть отрицательными. Например, k_x = -1 соответствует зеркальному отражению относительно оси y.

3. Поворот (рисунок 3).

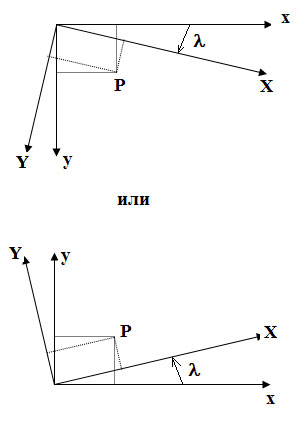
Рис.3. Поворот

Обратное преобразование соответствует повороту системы (X, Y) на угол (-λ).

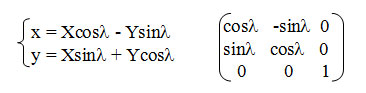
Свойства аффинного преобразования.

Любое аффинное преобразование может быть представлено как последовательность операций из числа указанных простейших: сдвиг, растяжение/сжатие и поворот.
Сохраняются прямые линии, параллельность прямых, отношение длин отрезков, лежащих на одной прямой, и отношение площадей фигур.

На следующем шаге мы рассмотрим аффинные преобразования в пространстве.

Предыдущий шаг Содержание Следующий шаг