На этом шаге мы рассмотрим несколько вариантов прямого вычисления координат.

    Пусть заданы координаты точек отрезка прямой. Найдем координаты точки внутри отрезка (рисунок 1).

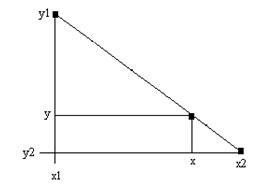
Рис.1. Отрезок прямой

    Запишем отношения катетов для подобных треугольников:

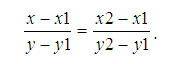
    Тогда:

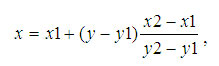
    А так же:

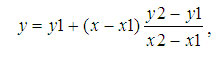
    В зависимости от угла наклона прямой выполняется цикл по оси x или по y (рисунок 2).

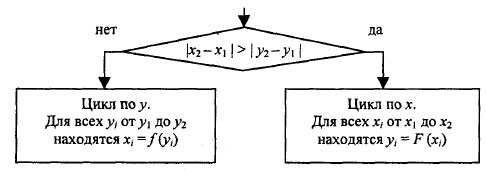
Рис.2. Алгоритм вывода отрезка прямой линии

    Приведем пример записи этого алгоритма. Для сокращения текста рассмотрим фрагмент программы, где выполняется цикл по оси x, причем x1<x2:

  for (x=x1; x<=x2; x++)
  {
    y = y1 + ((x-x1)*(y2-y1))/(x2-x1);
    SetPixel(x, y);
  }

    Здесь все операции выполняются над целыми числами. Двойные скобки необходимы для того, чтобы деление выполнялось после умножения. Недостатки такой программы - в цикле выполняется много лишних операций, присутствуют операции деления и умножения. Это обуславливает малую скорость работы. Относительно лишних операций в цикле. Можно вынести вычисление (y2-y1)/(x2-x1) из цикла, поскольку это значение не изменяется. Однако для этого уже необходимо использовать операции с плавающей точкой:

  float k;
  k = (float)(y2-y1)/(float)(x2-x1);
  for (x=x1; x<=x2; x++)
  {
    y = y1 + (float)(x-x1)*k;
    SetPixel (x, y);
  }

    Попробуем еще уменьшить количество операций в цикле. Если раскрыть скобки в выражении y = y1+(x-x1)*k, то получим y = y1 + x*k-x1*k. Здесь значение (y=y1-x1*k) является константой - эти операции также вынесем из тела цикла.

  float yy, k;
  k = (float) (y2-y1) / (float) (x2-x1);
  yy = (float) y1 - (float) x1*k;
  for (x=x1; x<=x2; x++)
  {
    y = yy + (float) x *k;
    SetPixel (x, y);
  }

    В цикле выполняются только две арифметические операции и преобразования x из целого в форму с плавающей точкой.

    Если рассматривать цикл вычисления y_i по соответствующим значениям x_i=x1, x1+1,…,x2 как итеративный процесс, то можно поставить такой вопрос: чему равна разность (y_i+1-y_i)? Она равна y_i+1-y_i = x1+(x_i+1-x1)k-x1-(x_i -x1)k = (x_i+1-x_i)k = k; поскольку (x_i+1-x_i)=1. Разность (y_i+1-y_i) - константа, равная k. Исходя из этого, можно построить цикл таким образом:

  float k;
  k = (float)(y2-y1)/(float)(x2-x1);
  y=y1;
  for (x=x1;x<=x2;x++)
 {
    y=y1+ (float)(x-x1)*k;
    SetPixel (x, y);
    y+=k;
  }

Рис.3. Результат работы приложения

    В теле цикла есть только одна операция для вычисления координаты y (если не учитывать <= и ++).

    Если сравнивать последний вариант с предыдущим, то последний лучше по быстродействию. Также существенно отличаются способы вычисления координаты у. В последнем варианте значение у вычисляется прибавлением приращения k на каждом шаге, и на последнем шаге цикла (когда x = x2) должно стать y = y2. Исходя из чисто математических соображений здесь все конкретно, однако необходимо учесть, что в компьютере дробные числа представляются в формате с плавающей точкой не точно. Кроме погрешности представления чисел существует ошибка выполнения арифметических операций с плавающей точкой. Ошибка зависит от разрядности мантисс, и самая малая - для long double, но все равно не нулевая. С каждым шагом цикла ошибки накапливаются, и может так произойти, что y не равно y2 на последнем шаге. Это необходимо учитывать при использовании алгоритма.

    Положительные черты прямого вычисления координат:

1. Простота, ясность построения алгоритма.
2. Возможность работы с нецелыми значениями координат отрезка.

    Недостатки:

1. Использование операций с плавающей точкой или целочисленных операций умножения и деления обуславливает малую скорость. Однако это зависит от процессора и для различных типов компьютеров может быть по-разному. В современных компьютерах, которых процессоры используют эффективные способы ускорения (например, конвейер арифметических операций с плавающей точкой), время выполнения целочисленных операций уже не намного меньше. Для старых компьютеров разница могла быть в десятки раз, поэтому и старались разрабатывать алгоритмы только на основе целочисленных операций.
2. При вычислении координат путем добавления приращений может накапливаться ошибка вычислений координат.

    Последнюю разновидность прямого вычисления координат, рассмотренную здесь, можно было бы назвать "инкрементной". Но такое название получили алгоритмы другого типа.

    На следующем шаге мы рассмотрим инкрементные алгоритмы.

Предыдущий шаг Содержание Следующий шаг