На этом шаге мы рассмотрим общий принцип работы таких алгоритмов.
Брезенхэм предложил подход, позволяющий разрабатывать так называемые инкрементные алгоритмы растеризации. Основной целью для разработки таких алгоритмов было построение циклов вычисления координат на основе только целочисленных операций сложения/вычитания без использования умножения и деления. Уже известны инкрементные алгоритмы не только для отрезков прямых, но и для кривых линий.
Инкрементные алгоритмы выполняются как последовательное вычисление координат соседних пикселей путем добавления приращений координат. Приращения рассчитываются на основе анализа функции погрешности. В цикле выполняются только целочисленные операции сравнения и сложения/вычитания. Достигается повышение быстродействия для вычислений каждого пикселя по сравнению с прямым способом. Один из вариантов алгоритма Брезенхэма:
xerr = 0, yerr =0;
dx = х2 - x1, dy = у2 - y1;
Если dx > 0, то incX = 1;
dx = 0, то incX = 0;
dx < 0, то incX = -1;
Если dy > 0, то incY = 1;
dy = 0, то incY = 0;
dy < 0, то incY = -1;
dx = |dx|, dy = |dy|;
Если dx > dy, то d = dx;
иначе d = dy;
x = x1, у = y1;
Пиксель (x, y)
Выполнить цикл d раз:
{
xerr = xerr + dx;
yerr = yerr + dy;
Если xerr > d, то xerr = xerr - d
x = x + incX
Если yerr > d, то yerr = yerr - d
у = у + incY
Пиксель (x, у)
}
Рассмотрим пример работы приведенного выше алгоритма Брезенхэма для отрезка (x1y1 - х2у2) = (2,3 - 8,6). Этот алгоритм восьмисвязный, то есть при вычислении приращений координат для перехода к соседнему пикселю возможны восемь случаев (рисунок 1).
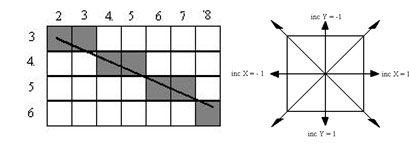
Рис.1. Восьмисвязность
Известны также четырехсвязные алгоритмы (рисунок 2).
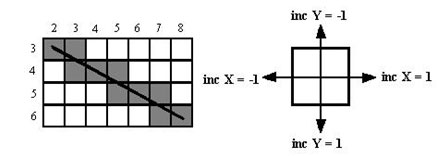
Рис.2. Четырехсвязность
Четырехсвязные алгоритмы проще, но они генерируют менее качественное изображение линий за большее количество тактов работы. Для приведенного примера четырехсвязный алгоритм работает 10 тактов, а восьмисвязный - только 7.
На следующем шаге мы рассмотрим алгоритм вывода окружности.
