На этом шаге мы приведем общие сведения об этой кривой.

    Разработана математиком Пьером Безье. Кривые и поверхности Безье были использованы в 60-х годах компанией "Рено" для компьютерного проектирования формы кузовов автомобилей. В настоящее время они широко используются в компьютерной графике.

    Кривые Безье описываются в параметрической форме:

  x = Px(t),
  y = Py(t).

    Значение t выступает как параметр, которому отвечают координаты отдельной точки линии. Параметрическая форма описания может быть более удобной для некоторых кривых, чем задание в виде функции y = f(х). Это потому, что функция f(х) может быть намного сложнее, чем P_x(t) и P_y(t), кроме того, f(х) может быть неоднозначной.

    Многочлены Безье для Р_х и Р_y имеют такой вид:

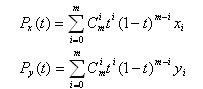
    Рассмотрим кривые Безье, классифицируя их по значениям m.

    m = 1 (по двум точкам).

    Кривая вырождается в отрезок прямой линии, определяемый концевыми точками Р₀ и Р₁ как показано на рисунке 1.

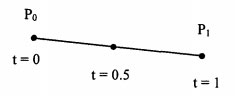
Рис.1. Кривая Безье (m=1)

    m = 2 (по трем точкам).

  P(t) = (1 - t)2 Р0 + 2t(1 - t) P1 + t2 Р2

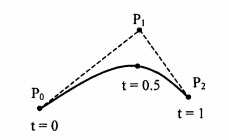
Рис.2. Кривая Безье (m=2)

    m = 3 (по четырем точкам, кубическая, рисунок 4)).

    Используется довольно часто, в особенности в сплайновых кривых.

  P(t) = (1 - t)3 Р0 + 3t(1 - t)2 P1 + 3t(1 - t)2 Р2 + t3 P3.

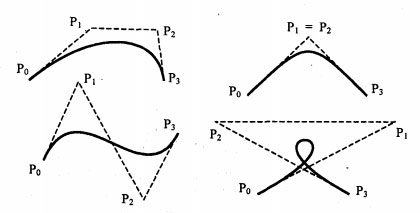
Рис.3. Кубические кривые Безье (m=3)

    На следующем шаге мы рассмотрим геометрический алгоритм для кривой Безье.

Предыдущий шаг Содержание Следующий шаг