На этом шаге мы рассмотрим алгоритм построения кривых Безье.
Этот алгоритм позволяет вычислить координаты (х, у) точки кривой Безье по значению параметра t. Алгоритм описан в [1].
- Каждая сторона контура многоугольника, проходящего по точкам-ориентирам, делится пропорционально значению t.
- Точки деления соединяются отрезками прямых и образуют новый многоугольник. Количество узлов нового контура на единицу меньше, чем количество узлов предыдущего контура.
- Стороны нового контура снова делятся пропорционально значению t. И так далее. Это продолжается до тех пор, пока не будет получена единственная точка деления. Эта точка и будет точкой кривой Безье (рисунок 1).
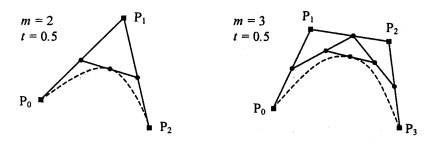
Рис.1. Геометрический алгоритм для кривых Безье
В качестве примера приложения, иллюстрирующего построение кривых Безье, возьмем немного переработанный пример, описанный в http://opita.net/node/50.
Для построения кривой Безье необходимо задать в клиентской области окна множество точек, используя мышь. Затем, после выбора пункта меню "Draw curve" можно изменять форму кривой с помощью мыши. Пункт меню "New curve" предназначен для удаления текущей кривой и выбора точек для построения новой.
Результат работы приложения изображен на рисунке 2.
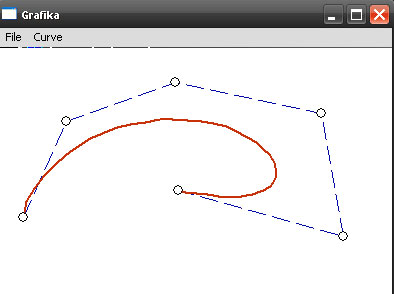
Рис.2. Результат работы приложения
Приведем текст основных функций приложения.
. . . . . #define false 0 #define true 1 typedef int bool; struct vector { int x; int y; }; . . . . . LRESULT CALLBACK WndProc(HWND hWnd, UINT message,WPARAM wParam, LPARAM lParam) { static bool IsSelected = false; // Булевская переменная, служащая для распознания, // выбран ли набор точек // для кривой или еще нет. Начальное значение - // "ложь", не выбран. static vector pts[20]; // Вектор-массив точек, по которым будем строить кривую. static int kol = -1; // Количество точек в массиве HDC hdc; // Контекст устройства. PAINTSTRUCT ps; switch(message) { case WM_LBUTTONDOWN: // Нажата левая кнопка мыши. // Если точки еще не выбраны, заносим координаты точки в массив и // рисуем окружность для выделения места нажатия. if (!IsSelected) { hdc = GetDC(hWnd); vector tmp; tmp.x = LOWORD(lParam); tmp.y = HIWORD(lParam); pts[++kol] = tmp; Ellipse(hdc, pts[kol].x-5, pts[kol].y-5, pts[kol].x+5, pts[kol].y+5); ReleaseDC(hWnd, hdc); } break; case WM_MOUSEMOVE: // Сообщение от перемещения мыши, обрабатывается только тогда, // когда выбран набор точек и // после отрисовки кривой (выбран пункт меню "Draw curve"). if (IsSelected) { // Если при перемещении мыши нажата левая кнопка, if (wParam && MK_LBUTTON) { hdc = GetDC (hWnd); // то находим номер точки массива, // если щелчок произвелся по одной из его точек. int mnp = GetNumberOfPoint(LOWORD(lParam), HIWORD(lParam), pts, kol); if (mnp < 0) break; // Заносим в точку массива с номером // выбранной точки новые координаты. pts[mnp].x = LOWORD (lParam) ; pts[mnp].y = HIWORD (lParam) ; // Посылаем сообщение для перерисовки клиентской области // окна, и, следовательно, самой кривой. SendMessage(hWnd, WM_PAINT, NULL, NULL); ReleaseDC (hWnd, hdc); } } break; case WM_COMMAND: switch (LOWORD(wParam)) { /*case 201: DrawStudyExample(hWnd); break;*/ case ID_CURVE_DRAWCURVE: // Меню Curve -> Draw curve // Если размер массива точек равен нулю, // т. е. пользователь не выбрал ни одной точки, то // выводим сообщение об ошибке. if (kol == -1) { MessageBox(hWnd, "There is necessary to put at least one point to client area of window!", "An error occured!", NULL); break; } // Иначе - присваиваем переменной IsSelected значение "истина" // (означающая, что пользователь выбрал набор точек) IsSelected = true; // и осуществляем перерисовку. SendMessage(hWnd, WM_PAINT, NULL, NULL); break; case ID_CURVE_NEWCURVE: // Меню Curve -> New curve // Очищаем массив точек, IsSelected присваиваем "ложь" // и осуществляем перерисовку. kol = -1; IsSelected = false; SendMessage(hWnd, WM_PAINT, NULL, NULL); break; case 108: DestroyWindow(hWnd); break; default: return DefWindowProc(hWnd, message, wParam, lParam); } break; case WM_PAINT: // Перерисовка клиенской области окна. // Объявление всей клиентской области подлежащей перерисовке. InvalidateRect(hWnd, NULL, TRUE); hdc = BeginPaint(hWnd, &ps); // Если массив точек не пуст, то рисуем кривую по данным точкам. if (kol != -1) DrawBezier(hdc, pts, kol) ; EndPaint(hWnd, &ps); break; case WM_DESTROY: PostQuitMessage(0); break; default:return DefWindowProc(hWnd,message,wParam,lParam); } return 0L; } // Функция отрисовки кривой Безье. // Принимает в качестве параметров дескриптор контекста устройства и // вектор-массив точек, по которым ведется построение кривой. void DrawBezier(HDC hdc, vector pts[], int kol) { double t; // Параметр, по которому будет идти вычисление точек на // кривой: t = [0,...,1]. HPEN hPen; // Дескриптор пера, которым будем пользоваться для сохранения // разных стилей рисования линий для построения // как отрезков, соединяющих // точки массива, так и самой кривой. POINT np = {0, 0}; // Точка, в которую будет заноситься результат // выполнения функции CalcBezierCurve. vector q[20]; for (int j=0;j<=kol;j++) q[j]=pts[j]; // Перемещаем текущую позицию пера в первую точку массива. MoveToEx(hdc, pts[0].x, pts[0].y, NULL); // Присваиваем перу характеристику: // пунктирная линия, толщина - 1 пиксель, синий цвет. hPen = CreatePen(PS_DASH, 1, RGB(0, 10, 170)); SelectObject(hdc, hPen); // Выбираем объект нашего пера в контекст устройства. // Строим пунктирные линии, соединяющие точки массива. for (int i = 0; i < kol+1; i++) LineTo(hdc, pts[i].x, pts[i].y); // Присваиваем перу характеристику: // сплошная линия, толщина - 2 пикселя, темно-красный цвет. hPen = CreatePen(PS_SOLID, 2, RGB(200, 50, 10)); SelectObject(hdc, hPen); // Выбираем объект нашего пера в контекст устройства. // Перемещаем текущую позицию пера в первую точку массива. MoveToEx(hdc, pts[0].x, pts[0].y, NULL); // Цикл отрисовки кривой Безье. // Для параметра t, пробегающего от 0 до 1 с шагом 0.3 // (данный шаг обеспечивает умеренную сглаженость кривой) // вычисляем значение новой точки и строим линию, // соединяющую предыдущую точку с новой. for (t = 0.0; t < 1.0; t += 0.03) { for (j=0;j<=kol;j++) pts[j]=q[j]; np = CalcBezierCurve(pts, t, kol); LineTo(hdc, np.x, np.y); } for (j=0;j<=kol;j++) pts[j]=q[j]; LineTo(hdc, pts[kol].x, pts[kol].y); // Возвращаем стандартное перо в контекст устройства. SelectObject(hdc, (HPEN)GetStockObject(BLACK_PEN)); // Рисуем окружности, выделяющие точки массива. for (i = 0; i < kol+1; i++) Ellipse(hdc, pts[i].x-5, pts[i].y-5, pts[i].x+5, pts[i].y+5); } // Функция, вычисляющая значение х и у координат точки на кривой. // Принимает в качестве параметров вектор-массив точек и // параметр t, характеризующий положение на кривой. POINT CalcBezierCurve(vector pts[], const double& t, int kol) { int i, c; double p; POINT np; int n = kol; c = 1; for (i = 0; i <= n; i++) { pts[i].x = pts[i].x * c; pts[i].y = pts[i].y * c; c = (n-i)*c/(i+1); } p = 1; for (i = 0; i <= n; i++) { pts[i].x = pts[i].x * p; pts[i].y = pts[i].y * p; p = p * t; } p = 1; for (i = n; i >= 0; i--) { pts[i].x = pts[i].x * p; pts[i].y = pts[i].y * p; p = p * (1-t); } np.x = 0; np.y = 0; for (i = 0; i <= n; i++) { np.x = np.x + pts[i].x; np.y = np.y + pts[i].y; } return np; } . . . . . // Функция, возвращающая номер точки массива, // по которой пользователь щелкает мышью. // Принимает в качестве параметров х и у координаты точки щелчка // и вектор-массив точек, задающих кривую. int GetNumberOfPoint (int x, int y, vector P[], int kol) { int lim = kol+1; // Проходим по массиву точек, for (int i = 0; i < lim; i++) { // Если щелчок произвелся по точке или // в непосредственной близости от нее, то if ((x > P[i].x-15 && x < P[i].x+15) && (y > P[i].y-15 && y < P[i].y+15)) // возвращаем номер этой точки (индекс в массиве). return i; } // Если щелчок произвелся не по точке массива, возвращаем отрицательное число. return -1; }
(1)Павлидис Т. Алгоритмы машинной графики и обработки изображений. - М.: Радио и связь, 1986.
На следующем шаге мы начнем рассматривать алгоритмы вывода фигур.
