Шаг 50.
Основы компьютерной графики. Базовые растровые алгоритмы. Стиль заполнения. Кисть. Текстура (еще продолжение)

    На этом шаге мы рассмотрим создание проективных текстур.

    Растровые текстуры и кисти широко используются в современной компьютерной графике, в том числе и в 3D-графике. Для отображения трехмерных объектов часто используются полигональные поверхности, каждая грань отображается с наложенной текстурой. Поскольку объекты обычно показываются с разных ракурсов - повороты, изменения размеров и тому подобное, то необходимо соответственно трансформировать и каждую грань с текстурой. Для этого используются проективные текстуры.

    Общая схема алгоритма заполнения контуров полигонов для проективных текстур такая же, как и приведенная на предыдущих шагах. Однако растровый образец здесь представляет всю грань, а преобразование координат из (х, у) в (xТ, yТ) более сложное, например, аффинное: 

  хТ = А х + B y + С,
  yТ = D x + E y + F,
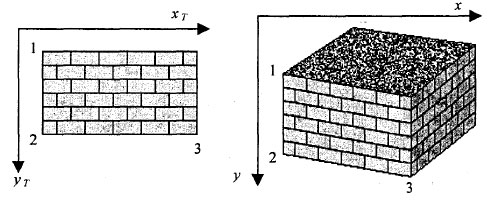
где коэффициенты А, В, ..., F - константы при пересчете координат всех пикселей для отдельной текстурированной грани. Такое преобразование координат можно использовать, если привязать текстуру к грани по трем опорным точкам. Пример наложения проективной текстуры приведен на рисунке 1.


Рис.1. Наложение проективной текстуры на две грани объекта

    Привязывание по трем точкам соответствует уравнениям: 

  хТi = А хi + B yi + С,
  yТi = D xi + E yi + F,
где i = 1, 2, 3. По известным координатам (хТi,yТi) и (х, у) можно найти коэффициенты А, В, ... , F, если решить систему линейных уравнений. Эта система распадается на две независимые системы третьего порядка. Для упрощения записи заменим хТi на Хi, а yТi на Yi: 
  X1 = A x1 + B y1 + C, 
  X2 = A x2 + B y2 + C, 
  X3 = A x3 + B y3 + C, 
                             и
  Y1 = D x1 + E y1 + F, 
  Y2 = D x2 + E y2 + F, 
  Y3 = D x3 + E y3 + F.

    Для решения систем линейных уравнений известно множество способов, пользуем способ, основанный на вычислении определителей. Решение первой системы для коэффициентов А, В и С можно записать в виде 

  А = detA / det,
  В = detB / det,
  С = detC / det,
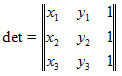где - это главный определитель системы, а определители detA, detB и detC получаются заменой соответствующих столбцов в det столбцом свободных членов:

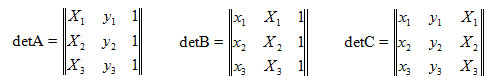
    Если главный определитель равен нулю, то это означает, что решение сисмы невозможно. Это может быть, например, тогда, когда все три точки (х1, у1), (х2, у2) и (х3, у3) располагаются вдоль прямой линии (грань вид с торца). Однако в этом случае рисовать текстуру и не нужно. Вычислить определитель третьей степени можно, например, по "правилу Саррюса" [1]. Для этого справа нужно дописать первые два столбца, а затем сложить (вычесть) произведения по диагоналям:

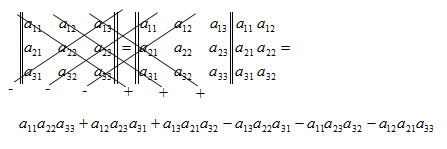
    Вычислим главный определитель:

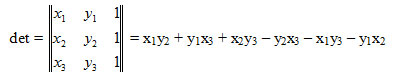
    Преобразуем выражение так, чтобы уменьшить число умножений: 

  det = x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)

    Аналогично вычисляются определители detA и detB. Определитель detC является самым сложным из всех. Но его вычислять не обязательно. Запишем решение системы в следующем виде: 

  А = detA / det = (Х1 (y2 - y3) + Х2 (y3 - y1) + Х3 (y1 - y2)) / det,
  В = detB / det = (x1 (Х2 - Х3) + х2 (Х3 - Х1) + х3 (Х1 - Х2)) / det,
  С = Х1 - А x1 - В у1.

    Таким же способом решаем систему уравнений для D, E и F. 

  D = (Y1 (y2 - y3) + Y2 (y3 - у1) + Y3 (y1 - y2)) / det,
  E = (x1 (Y2 - Y3) + х2 (Y3 - Y1) + х3 (Y1 - Y2)) / det,
  F = Y1 - D x1 - E y1.

    Заметьте, что здесь главный определитель det совпадает с определителем первой системы уравнений - для А, В и С.

(1)Бронштейн И.Н., Семендяев К.А. Справочник по математике. - М., Л.: ОГИЗ, 1948. - 556 с.

    На следующем шаге мы закончим изучение этого вопроса.




Предыдущий шаг Содержание Следующий шаг