На этом шаге мы рассмотрим особенности данной модели.

Начиная с этого шага,мы рассмотрим методы, которые позволяют получить более-менее реалистичные изображения для объектов, моделируемых многогранниками и полигональными сетками. Эти методы достаточно подробно описаны в [1, 2, 3], а также в [4, 5].

Рассмотрим, как можно определить цвет пикселей изображения поверхности согласно интенсивности отраженного света при учете взаимного расположения поверхности, источника света и наблюдателя.

Зеркальное отражение света

Угол между нормалью и падающим лучом (θ) равен углу между нормалью и отраженным лучом. Падающий луч, отраженный, и нормаль располагаются в одной плоскости (рисунок 1).

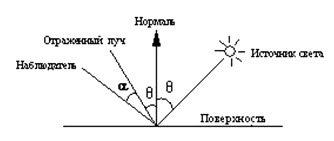
Рис.1. Зеркальное отражение света

Поверхность считается идеально зеркальной, если на ней отсутствуют какие-либо неровности, шероховатости. Собственный цвет у такой поверхности не наблюдается. Световая энергия падающего луча отражается только по линии отраженного луча. Какое-либо рассеяние в стороны от этой линии отсутствует. В природе, вероятно, нет идеально гладких поверхностей, поэтому полагают, что если глубина шероховатостей существенно меньше длины волны излучения, то рассеивания не наблюдается. Для видимого спектра можно принять, что глубина шероховатостей поверхности зеркала должна быть существенно меньше 0,5 мкм [6].

Если поверхность зеркала отполирована неидеально, то наблюдается зависимость интенсивности отраженного света от длины волны - чем больше длина волны, тем лучше отражение. Например, красные лучи отражаются сильнее, чем синие.

При наличии шероховатостей имеется зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов (θ), близких к 90 градусам [6, 7].

Падающий луч, попадая на слегка шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, рассеиваемых по различным направлениям. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но достаточно используемых, относится эмпирическая модель распределения Фонга, согласно которой интенсивность зеркально отраженного излучения пропорциональна (cos α)^p, где α - угол отклонения от линии идеально отраженного луча. Показатель p находится в диапазоне от 1 до 200 и зависит от качества полировки [2]. Запишем это таким образом:

 I_s = I K_scos^pα,

где I - интенсивность излучения источника, K_s - коэффициент пропорциональности.

⁽¹⁾Иванов В.П., Батраков А.С. Трехмерная компьютерная графика. -М.: Радио и связь, 1995. - 223 с.
⁽²⁾Фоли Дж., ван Дэм А. Основы интерактивной машинной графики. В 2-х книгах. - М.: Мир, 1985.
⁽³⁾Шикин Е.В., Боресков А.В. Компьютерная графика. - М.: ДИАЛОГ-МИФИ, 1995.
⁽⁴⁾3D Studio MAX R3. Справочная документация. Autodesk Inc.,1999.
⁽⁵⁾Bryce 4. User Guide. MetaCreations Corporation. 1999
⁽⁶⁾Хвольсон О.Д. Курс физики. В пяти томах. Издание пятое. Том второй. - Берлин, Государственное издательство, 1923. - 774 с.
⁽⁷⁾Кошкин Н.И., Ширкевич М.Г. Справичник по элементарной физике. - М.:Наука, 1980. - 208 с.

На следующем шаге мы рассмотрим диффузное отражение.

Предыдущий шаг Содержание Следующий шаг