На этом шаге мы приведем решение этой задачи.

    Сформулируем задачу следующим образом. Заданы два единичных вектора: S₁ - это радиус-вектор, направленный на источник, и N₁ - радиус-вектор нормали к границе раздела двух сред. Также должны быть известны два коэффициента преломления для данных сред - n₁ и n₂ (или же их отношение).

    Требуется найти единичный радиус-вектор преломленного луча Т₁. Для решения этой задачи выполним некоторые геометрические построения (рисунок 1).

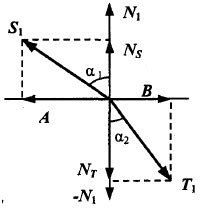
Рис.1. Преломление

    Нанесем еще несколько радиус-векторов (далее мы их все для краткости будем называть векторами).

    Искомый вектор T₁ равен сумме двух векторов: T₁=N_T + В.

    Найдем вначале вектор N_T. Он противоположен по направлению вектору нормали, а его длина равна |T₁| cos α₂ = cos α₂ (поскольку по условию задачи Т₁ - единичный). Таким образом, N_T = -N₁ cos α₂. Необходимо определить cos α₂. Запишем закон преломления n₁ sin α₁ = n₂ sin α₂ в виде:

  sin α2 = n sin α1

    Воспользуемся тождеством cos²x +sin²x = 1. Тогда

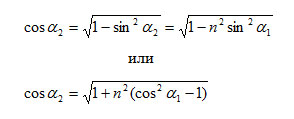
    Значение cos α₁ можно выразить через скалярное произведение единичных векторов S₁ и N₁, то есть cos α₁ = S₁ * N₁. Тогда мы можем записать такое выражение для вектора N_T:

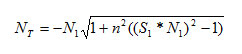
    Осталось найти выражение для вектора В. Он располагается на одной прямой с вектором А, причем А = S₁ - N_S. Учитывая, что вектор N_S равен N₁ cos α₁, то A = S₁ - N₁ cos α₁. Так как cos α₁ = S₁ * N₁, то A = S₁ - N₁ (S₁ - N₁).

    Поскольку длина вектора А равна sin α₁, a длина вектора В равна sin α₂, то

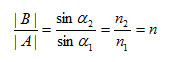
    Теперь мы можем записать искомое выражение для единичного радиус-вектора луча преломления Т₁:

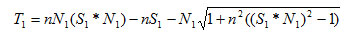
    Если подкоренное выражение отрицательно, то преломленный луч не существует. Это соответствует так называемому полному внутреннему отражению [1, 2, 3].

    Это решение задачи в векторном виде. Используя полученное выражение, можно записать координаты вектора T₁.

    На следующем шаге мы рассмотрим трассировку лучей.

Предыдущий шаг Содержание Следующий шаг