На этом шаге мы приведем некоторые теоретические положения.

    В заключение рассмотрим еще некоторые теоретические аспекты. На рисунке 1 показаны локальные координаты.

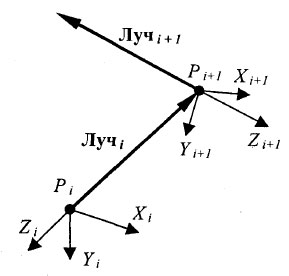
Рис.1. Локальные координаты для текущих лучей

    Пусть из точки P_i выпущен i-й луч, который пересек ближайший объект в точке Р_i+1. Координаты точки Р_i+1 в системе координат (X_i, Y_i, Z_i) равны (0, 0, z_p). Предположим, что направление нового, (i+1)-го, луча определяется в виде параллельного ему радиус-вектора в этой же системе координат, то есть (X_i, Y_i, Z_i). Обозначим координаты этого радиус-вектора через (x_r, y_r, z_r). Как определить новую систему координат, связанную с (i+1)-м лучом? Эту систему координат можно получить следующим образом. Вначале сдвинуть систему (X_i, Y_i, Z_i) по оси Z, на величину z_p, а затем выполнить поворот так, чтобы ось Z_i+1 была бы направлена против нового луча. Запишем формулы преобразований в следующем виде:

  Xi+1 = Xi cos α - Yi sin α
  Yi+1 = Xi sin α cos β + Yi cos α cos β - (Zi - zp) sin β
  Zi+1 = Xi sin α sin β + Yi cos α sin β - (Zi - zp) cos β

    Выразим поворот не углами, а через координаты радиус-вектора, который указывает новое направление оси Z. Рассмотрим рисунок 2.

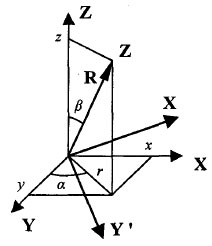
Рис.2. Поворот осей

    Пусть радиус-вектор имеет координаты (х, у, z). Длина радиус-вектора равна R:

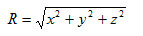
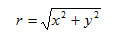
    Тогда:

  cos α = y / r,
  sin α = x / r,
  cos β = z / R,
  sin β = r / R   .

    Подставим эти значения в формулы преобразования координат, учитывая, что радиус-вектор нового трассируемого луча направлен противоположно направлению оси Z_i+1 то есть (х, у, z) = (-x_r, -y_r, -z_r). Запишем формулы в следующем виде:

  Xi+1 = -Xi (yr / r) + Yi (xr / r),
  Yi+1 = Xi (xr / r) (zr / R) + Yi (yr / r) (zr / R) - Zi (r / R) + zp (r / R),
  Zi+1 = -Xi (xr / R) - Yi (yr / R) - Zi (zr / R) + zp) (zr / R).

    В матричной форме:

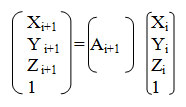
    Матрица A_i+i соответствует аффинному преобразованию сдвига и поворота. В ходе трассировки лучей нам необходимо выполнять преобразования из мировой системы в систему координат текущего луча. Обозначим матрицу преобразований через М_i+1:

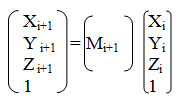
    Поскольку М₁ = А₁, то

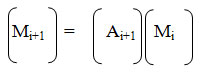
    Таким образом, матрица для системы координат нового луча образуется умножением матрицы предыдущего луча на матрицу сдвига и поворота.

    Важным моментом при расчетах отражения и преломления является определение нормали к видимой для текущего трассируемого луча стороны участка поверхности (рисунок 3).

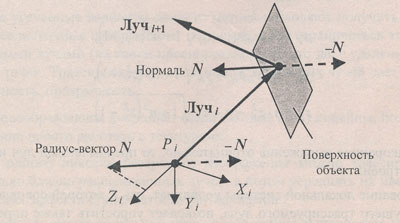
Рис.3. К выбору нормали видимой стороны объекта

    Введение локальной системы координат значительно упрощает такой выбор направления нормали. Можно руководствоваться следующим правилом - среди двух противоположно направленных векторов нормали (N и -N) выбирается тот, у которого соответствующий радиус-вектор в локальной системе координат (X_i, Y_i, Z_i) имеет положительную координату Z.

    Рассмотрим вычисление вектора зеркально отраженного луча (Луч_i+1). Для этого воспользуемся уже известной нам векторной формулой, которую здесь запишем для единичных векторов: R = 2 N (N * S) - S. Вычисляемый по этой формуле вектор R направлен так же, как искомый вектор Луч_i+1, а единичный вектор S нацелен противоположно вектору падающего луча, то есть вектору Луч_i.

    Еще раз подчеркнем, что речь здесь идет о лучах обратной трассировки, для которой падающий и отраженный лучи имеют противоположный смысл световым лучам, распространяемым в реальном случае.

    Координаты вектора S составляют (0, 0, 1) в локальной системе. Обозначим координаты единичного вектора нормали N через (x_N, y_N, z_N). Найдем вначале скалярное произведение (N * S) = (0 * x_N, 0 * y_N, 1 * z_N) = z_N. Координаты вектора отраженного луча (R) составляют:

  xr = 2 xN zN,
  yr = 2 yN zN,
  zr = 2 zN zN - 1   .

    Очевидно, что направление вектора не изменится, если все его координаты разделить на два. Тогда можно записать для координат радиус-вектора отраженного луча (Луч_i+1 = 0.5 R) такие формулы:

  xr = xN zN,
  yr = yN zN,
  zr = zN zN - 0.5   .

    Теперь займемся вычислением координат преломленного луча. Для этого воспользуемся формулой идеального (зеркального) преломления:

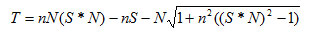
    Так как вектор S = (0, 0, 1), то:

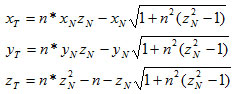
    Если подкоренное выражение отрицательно, то преломленный луч не может быть построен.

    Использование локальной системы координат, ось Z которой совпадает с линией текущего трассируемого луча, позволяет упростить также определение пересечения с оболочкой объекта. Наиболее просто определяется пересечение луча с оболочкой-шаром. Поскольку в любой локальной системе координат, задаваемой линейными преобразованиями, проекция шара есть круг, то достаточно узнать локальные координаты центра круга (Хс и Yc) и проверить, выполняется ли следующее соотношение: (Xc)² + (Yc)² ≤ (радиус оболочки)². Если выполняется, то текущий луч пересекает оболочку.

    В качестве оболочки можно использовать и другую форму, например цилиндр или параллелепипед. Поскольку определение пересечения луча с произвольно повернутым цилиндром или параллелепипедом уже не столь простая задача, то здесь можно использовать следующее. Хотя расположение осей координат X, Y локальной системы ранее было нам безразлично (главное, чтобы ось Z лежала бы на линии луча), но, оказывается, приведенные выше формулы преобразования координат для локальной системы обеспечивают сохранение одинаковой ориентации для вертикальных линий. Ранее мы уже отмечали это свойство выбранного способа поворота осей применительно к аксонометрической проекции. Поэтому возможно определить проекции оболочки для всех поворотов локальных систем координат в виде прямоугольника некоторых размеров в плоскости (X0Y). Определение пересечения луча с оболочкой сводится к проверке, находится ли точка локальных координат (Х_i, Y_i) = (0, 0) внутри прямоугольника, описывающего оболочку.

    А теперь сделаем общие выводы по методу обратной трассировки лучей. Положительные черты:

1. Универсальность метода, его применимость для синтеза изображений достаточно сложных пространственных схем. Воплощает многие законы геометрической оптики. Просто реализуются разнообразные проекции.
2. Даже усеченные варианты данного метода позволяют получить достаточно реалистичные изображения. Например, если ограничиться только первичными лучами (из точки проецирования), то это дает удаление невидимых точек. Трассировка уже одного-двух вторичных лучей дает тени, зеркальность, прозрачность.
3. Все преобразования координат (если таковые есть) линейны, поэтому достаточно просто работать с текстурами.
4. Для одного пикселя растрового изображения можно трассировать несколько близко расположенных лучей, а потом усреднять их цвет для устранения эффекта ступенчатости (антиалиасинг).
5. Поскольку расчет отдельной точки изображения выполняется независимо от других точек, то это может быть эффективно использовано при реализации данного метода в параллельных вычислительных системах, в которых лучи могут трассироваться одновременно.

    Недостатки:

1. Проблемы с моделированием диффузного отражения и преломления.
2. Для каждой точки изображения необходимо выполнять много вычислительных операций. Трассировка лучей относится к числу самых медленных алгоритмов синтеза изображений.

    Со следующего шага мы начнем рассматривать примеры изображения трехмерных объектов.

Предыдущий шаг Содержание Следующий шаг