На этом шаге мы рассмотрим общие принципы построения каркасного изображения шара.
Рассмотрим несколько способов построения изображения шара.
Для каркасного изображения шара можно рисовать сетку меридианов и параллелей. Для этого удобно воспользоваться известными формулами параметрического описания. Координаты точек поверхности шара определяются как функции от двух переменных (параметров) - широты и долготы (рисунок 1):
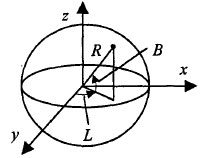
Рис.1. Широта и долгота
x = R cos В sin L, y = R cos В cos L, z = R sin В,
Меридиан - это линия, представляющая точки с постоянной долготой. Каркас из меридианов можно нарисовать следующим образом:
for (L=0; L<360; Ll+=dL) for (B=-90; B<=90; B+=dB) { x = R cos В sin L ; у = R cos В cos L ; z = R sin В ; (X, Y) = Преобразование координат (х, у, z); Рисование отрезка до точки (X, Y); }
Здесь введены две величины - dL и dB. Значение dL определяет шаг меридианов по долготе, значение dB - это шаг по широте, который должен быть малым (единицы градусов) для изображения меридиана достаточно гладкой кривой. Преобразование координат производится по формулам, соответствующим выбранной проекции. Для аксонометрической проекции - это поворот мировых координат на углы α и β с последующим преобразованием видовых координат в экранные координаты (шаг 19).
Параллель - это линия, состоящая из точек с постоянной широтой. Для рисования каркаса из параллелей можно использовать такой цикл:
for (В=-90; В<=90; B+=dB) for (L=0; L<=360; Ll+=dL) { x = R cos В sin L ; у = R cos В cos L ; z = R sin В ; (X, Y) = Преобразование координат (x, у, z); Рисование отрезка до точки (X, Y); }
На рисунке 2 изображены примеры каркасного изображения на основе меридианов и параллелей.
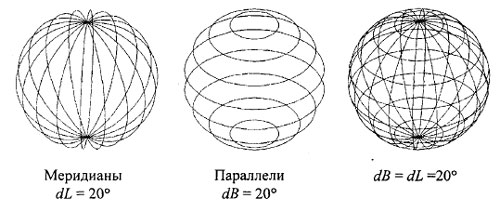
Рис.2. Меридианы и параллели
На следующем шаге мы рассмотрим удаление невидимых точек.
