На этом шаге мы рассмотрим этот алгоритм.
Метод Гуро дает хорошие результаты для создания иллюзии гладкой поверхности шара, изображаемого достаточно большим числом плоских граней. В соответствии с этим методом для каждой грани нужно определить векторы в вершинах, затем для каждой вершины вычислить значение интенсивности отраженного света и потом, при выводе полигона грани, интерполировать интенсивности вершин для вычисления интенсивности отраженного света в каждой точке внутри грани.
Значительным удобством при вычислении координат нормалей в вершинах граней в нашем случае является то, что координаты вектора нормали в любой вершине грани совпадают с координатами самих вершин - если центр шара имеет координаты (0, 0, 0).
Рассмотрим случай, когда точечный источник света расположен на оси Z видовых координат. Используем диффузную модель отражения. В этом случае рассчитать интенсивность отраженного света в вершине грани можно следующим образом. Косинус угла между осью Z и нормалью:
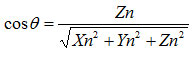
Поскольку координаты вектора нормали в вершине равны координатам вершин, а сумма квадратов координат (в том числе и видовых) для любой точки поверхности шара равна квадрату его радиуса, то:
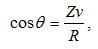
Алгоритм вывода многогранника для метода Гуро аналогичен рассмотренному на предыдущем шаге алгоритму. Запишем его следующим образом:
for (В=-90; B<90; B+=dB) for (L=0; L<360; L+=dL) { Определение мировых координат вершин грани х[i], у[i], z[i]. Поворот координат х[i], у[i], z[i] для определения видовых координат X[i], Y[i], Z[i]. Вычисление интенсивности отраженного света в вершинах. В простейшем случае для диффузного рассеивания Iотр[i] = Iист * Z[i] / R. Преобразование видовых координат в координаты устройства графического вывода (экранные координаты). Рисование полигона с интерполяцией интенсивностей. }
На рисунке 1 представлены многогранники с различным числом граней, закрашенные в соответствии с методом Гуро.
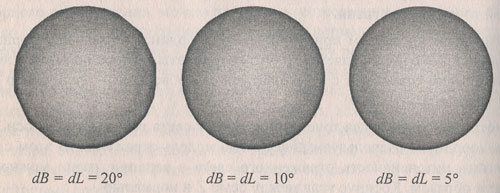
Рис.1. Закрашивание Гуро
Как видно на рисунке 1, иллюзия гладкости поверхности достигается уже при достаточно малом числе граней. Так, например, при dB = dL = 20° в большей степени заметны неровности контура, чем погрешности закрашивания.
На следующем шаге мы рассмотрим учет расположения источника света.
