На этом шаге мы рассмотрим общий алгоритм закраски.
Построим изображение так, чтобы грани были окрашены в соответствии с законами отражения света. Общую схему алгоритма можно изобразить таким образом:
for (В=-90; В<90; B+=dB) for (L=0; L<360; Ll+=dL) { x[0] = R cos B sin L; y[0] = R cos В cos L; z[0] = R sin В; х[1] = R cos (B+dB) sin L; y[1] = R cos (B+dB) cos L; z[1] = R sin (B+dB); х[2] = R cos (B+dB) sin (L+dL); y[2] = R cos (B+dB) cos (L+dL); z[2] = R sin (B+dB); х[3] = R cos В sin (L+dL) ; y[3] = R cos В cos (L+dL); z[3] = R sin В; (X [i] , Y[i], Z[i] ) = Поворот координат (x[i], y[i], z[i]); Определение вектора нормали по (X[i], Y[i], Z[i]) и определение цвета грани, учитывающего ее ориентацию относительно источника света. Рисование выбранным цветом полигона грани с четырьмя вершинами (X[i], Y[i], Z[i]); }
Приведенную тут схему алгоритма не следует воспринимать как программу на языке С, а также сам алгоритм как оптимальный. В частности, здесь много лишних вычислений косинусов и синусов - количество таких операций обязательно нужно уменьшать, поскольку они выполняются в традиционных компьютерах очень медленно. Кроме того, здесь и далее мы будем рисовать все грани четырехугольниками, хотя, лишь незначительно усложнив данную схему, можно предусмотреть и отдельную ветвь для треугольных граней у полюсов.
Для удаления невидимых точек можно использовать Z-буфер, но можно перестроить цикл так, чтобы грани рисовались в таком порядке - начиная с самых дальних и заканчивая ближайшими.
Для определения цвета каждой грани нужно учесть взаимное расположение источника света и нормали грани. Как уже было показано на предыдущих шагах для диффузной и зеркальной моделей отражения, важно определить координаты вектора нормали. Мы уже рассматривали общий способ вычисления координат нормали к произвольной плоской грани (шаг 69). Этот способ, на основе векторного произведения, можно применить, естественно, и в данном случае. Однако для таких многогранников как наши, нормали к граням можно вычислять значительно проще и быстрее. Поскольку радиус-вектор для каждой точки поверхности шара и есть вектор нормали, то координаты каждой точки поверхности шара являются координатами вектора нормали, если координаты центра шара равны (0, 0, 0). Таким образом, для вычисления координат вектора нормали к грани достаточно определить координаты точки поверхности шара, соответствующей центру грани. Или же можно взять сумму координат вершин грани и разделить на число вершин - это уже приближенный неточный способ.
На рисунке 1 изображены многогранники с различным числом граней, причем источник освещения расположен сзади нас - на оси Z видовых координат.
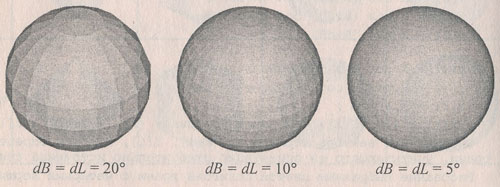
Рис.1. Закрашивание граней с учетом их ориентации
Как видим, для создания иллюзии гладкой поверхности шара нужно очень большое число граней (очевидно, что это число возрастает с увеличением видимого радиуса шара). Если рассматривать рисунок 1, то при dB = dL = 5° многогранник уже похож на шар - отдельные грани на рисунке достаточно сложно различить.
Однако на экране дисплея грани все еще заметны. Глаз человека подчеркивает границы.
На следующем шаге мы рассмотрим закрашивание граней методом Гуро.
