На этом шаге мы рассмотрим несколько примеров.
Приведем несколько примеров решения некоторых упражнений.
Пример 1. Напишите индуктивное определение функции len: A*→ N, позволяющей найти длину слова в алфавите A.
Решение. Вначале выскажем гипотезу об индуктивном определении:
len: A*→ N и
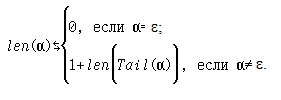
Разумеется, для подтверждения гипотезы необходимо привести доказательство.
Предложение. Функция len: A*→ N, определённая следующим индуктивным образом:
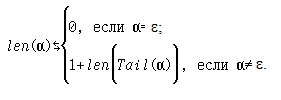
Доказательство. Воспользуемся полной индукцией по количеству букв в слове.
Очевидно, что len(ε)=0 (база индукции), т.к. пустое слово - это слово, не содержащее букв.
Докажем, что если функция правильно вычисляет длину слова α', имеющего на одну букву меньше, чем слово α, то функция len правильно вычисляет длину слова α. Пусть len(α')=n (гипотеза индукции).
Докажем, что len(α)=n+1. Т.к. n+1 ≥ 1, то α ≠ ε. Следовательно, len(α) = len(Tail(α))+1.
Известно, что функции Head(α) и Tail(α) определены, т.к. α ≠ ε, однако Tail(α) содержит все буквы слова α, кроме первой. Поэтому по гипотезе индукции можно предполагать, что len(Tail(α))=n.
Таким образом, добавив одну букву (Head(α)) к слову Tail(α), мы получим исходное слово α, причём len(α)=n+1.
Предложение доказано.
Теперь мы можем синтезировать программу на языке функционального программирования LISP из индуктивного определения. Другими словами, теперь можем записать индуктивное определение на языке LISP:
(DEFUN Len (LAMBDA (LST)
(COND ( (NULL LST) 0 )
( T (+ 1 (Len (CDR LST))) ))))
Мы можем также синтезировать программу на языке продукционного программирования Рефал из индуктивного определения. Другими словами, можем записать индуктивное определение следующим образом:
$use STDIO;
$use ARITHM;
$func Len e = s;
Main {
= <Print "Введите слово: ">,
<PrintLn "Количество букв в слове: "
<Len <Read-Line>>>;
};
Len {
e1 s2 e3 = <"+" 1 <Len e3>>;
e1 = 0;
};
Пример 2. Напишите индуктивное определение функции Last: A+→ A, позволяющей найти последнюю букву слова в алфавите A.
Решение. Вначале выскажем гипотезу об индуктивном определении:

Разумеется, для подтверждения гипотезы необходимо привести доказательство.
Предложение. Построенное индуктивное определение правильно.
Доказательство. Воспользуемся индукцией по длине слова α.
Пусть len(α)=1. Тогда по базисному пункту индуктивного определения значение Last(α) совпадает с α, т.е. с единственной буквой.
Пусть для всех слов, длина которых меньше некоторого натурального n>1, построенное индуктивное определение правильно.
Рассмотрим слово a+α, длина которого равна n. Тогда из индуктивного определения Last(a+α) ⇔ Last (α), а по сделанному предположению Last(α) возвращает последнюю букву слова α.
Предложение доказано.
Теперь мы можем синтезировать программу на языке функционального программирования LISP из индуктивного определения. Другими словами, можем записать индуктивное определение на языке LISP:
(DEFUN Last (LAMBDA (LST)
(COND ( (NULL (CDR LST)) (CAR LST) )
( T (Last (CDR LST)) ))))
Запись индуктивного определения на языке программирования Рефал:
$use STDIO;
$func Last e = e;
Main {
= <Print "Введите слово: ">,<Read-Line>::e1,
<PrintLn <Last e1>>;
};
Last {
s1 = s1;
s1 e2 = <Last e2>;
};
Пример 3. Напишите индуктивное определение предиката =: A* ×A*→ B2, устанавливающего равенство двух заданных слов α, β ∈ A*.
Решение. Вначале выскажем гипотезу об индуктивном определении:
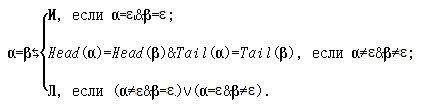
Разумеется, для подтверждения гипотезы необходимо привести доказательство (проведите его самостоятельно).
Теперь мы можем синтезировать программу на языке функционального программирования LISP из индуктивного определения. Другими словами, можем записать индуктивное определение на языке LISP:
(DEFUN = (LAMBDA (LST1 LST2)
(COND ( (AND (NULL LST1) (NULL LST2)) T )
( (AND (NOT (NULL LST1)) (NOT (NULL LST2)))
(AND (EQ (CAR LST1) (CAR LST2))
(= (CDR LST1) (CDR LST2))) )
( T NIL ))))
Запись индуктивного определения на языке программирования Рефал:
$use STDIO;
$func Rav e (e) = e;
Main {
= <Print "Введите два слова: ">,<Read-Line>::e1,
<Read-Line>::e2,<PrintLn <Rav e1 (e2)>>;
};
Rav {
() = <Print "Слова равны.">;
s1 e2 (s1 e3) = <Rav e2 (e3)>;
e2 (e3) = <Print "Слова не равны.">;
e1 () = <Print "Слова не равны.">;
(e1) = <Print "Слова не равны.">;
};
Пример 4. Напишите индуктивное определение алгебраической операции °: A*× A*→ A*, позволяющей приписать слово β ∈ A* к слову α ∈ A*.
Решение. Пусть a + α обозначает результат операции левого присоединения буквы a ∈ A к слову α. Тогда можно высказать гипотезу об индуктивном определении:
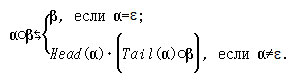
Разумеется, для подтверждения гипотезы необходимо привести доказательство.
Предложение. Построенное индуктивное определение правильно.
Доказательство. Воспользуемся индукцией по длине слова α.
Пусть len(α)=0. Тогда по базисному пункту индуктивного определения значение α ° β совпадает с β.
Пусть для всех слов, длина которых меньше некоторого натурального n>0, построенное индуктивное определение правильно.
Рассмотрим слово a + α, длина которого равна n. Тогда из индуктивного определения α ° β = (a + α1) ° β ⇔ a + (α ° β), а по сделанному предположению α1 ° β возвращает конкатенацию слов α1 и β. Остаётся не забыть приписать вначале букву a и получить конкатенацию слов α и β.
Предложение доказано.
Теперь мы можем синтезировать программу на языке функционального программирования LISP из индуктивного определения. Другими словами, можем записать индуктивное определение на языке LISP:
(DEFUN ConCat (LAMBDA (LST1 LST2)
(COND ( (NULL LST1) LST2)
( T (CONS (CAR LST1) (ConCat (CDR LST1) LST2)) ))
))
Запись индуктивного определения на языке программирования Рефал:
$use STDIO;
$func ConCat e (e) = e;
Main {
= <Print "Введите два слова: ">,<Read-Line>::e1,
<Read-Line>::e2,<PrintLn <ConCat e1 (e2)>>;
};
ConCat {
(e1) = e1;
s1 e2 (e3) = s1 <ConCat e2 (e3)>;
};
На следующем шаге мы продолжим изучение этого вопроса.
