На этом шаге мы продолжим рассмотрение таких примеров.
Пример 5. Напишите индуктивное определение функции Reverse: A*→ A*, позволяющей осуществить обращение слова a ∈ A*.
Решение. Вначале выскажем гипотезу об индуктивном определении:
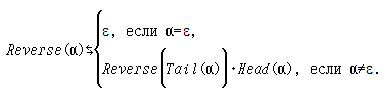
Разумеется, для подтверждения гипотезы необходимо привести доказательство (проведите его самостоятельно).
Теперь мы можем синтезировать программу на языке функциональногопрограммирования LISP из индуктивного определения. Другими словами, можем записать индуктивное определение на языке LISP с использованием встроенных функций APPEND и LIST:
(DEFUN Reverse1 (LAMBDA (LST)
(COND ( (NULL LST) NIL )
( T (APPEND (Reverse1 (CDR LST)) (LIST (CAR LST))) ))
))
Запись индуктивного определения на языке программирования LISP без использования встроенных функций APPEND и LIST такова:
(DEFUN Reverse1 (LAMBDA (LST)
(COND ( (NULL LST) NIL )
( T (ConCat (Reverse1 (CDR LST))
(CONS (CAR LST) NIL)) ))))
; ----------------------------------------------
(DEFUN ConCat (LAMBDA (LST1 LST2)
(COND ( (NULL LST1) LST2 )
( T (CONS (CAR LST1) (ConCat (CDR LST1) LST2)) ))))
Запись индуктивного определения на языке программирования Рефал:
$use STDIO;
$func Reverse1 e = e;
Main {
= <Print "Введите слово: ">,<READ-LINE>::e1,
<PrintLn <Reverse1 e1>>;
};
/* ----- */
Reverse1 {
s.X e.Rest = <Reverse1 e.Rest> s.X;
= ;
};
Пример 6. Определите семантику и докажите правильность индуктивного определения следующей функции:
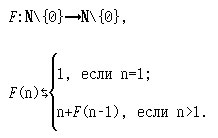
Решение.
Предложение. Определение описывает функцию, вычисляющую сумму n первых натуральных чисел; другими словами,
F(n)=n+(n-1)+ ...+1 = n(n+1)/2.
Доказательство. Воспользуемся натуральной индукцией.
F(1)=1 (база индукции).
Предположим, что функция правильно вычисляет сумму n первых положительных целых чисел для каждого из чисел 1,2,...n.
Докажем (для любого положительного числа n), что если справедливо равенство F(n)=n(n+1)/2 (предположение индукции), то
F(n+1)=(n+1)+n+(n-1)+...+1=(n+1)*((n+1)+1)/2.
Так как n - положительное число, то n+1>1 и
F(n) ⇔ n + F(n-1) ⇔ n+(n-1)n/2=(2n+n2-n)/2=n(n+1)/2.
Предложение доказано.
Попутно доказана правильность следующей функции, написанной на языке функционального программирования LISP:
(DEFUN F (LAMBDA (N)
(COND ( (EQ N 1) 1 )
( T (+ N (F (- N 1))) ))
))
Пример 7. Рассмотрим следующее рекурсивное определение числовой функции (эту функцию привёл в качестве примера Дж.Маккарти, и обычно ее называют функцией-91 Маккарти), n ∈ Z:

Докажите, что

Решение. Базисный пункт индуктивного определения относится кзначениям аргумента n>100, поэтому рассмотрим множество
M ⇔ {n¦n ∈ Z & n ≤ 100}
На множестве, упорядоченном указанным образом, с помощью принципа трансфинитной индукции докажем, что

Очевидно, что если n>100, то F(n)=n-10.
Таким образом, остается показать, что F(n)=91 при n≤100.
При использовании принципа трансфинитной индукции, необходимо доказать, что:
(1) F(n)=91 для наименьшего элемента множества M. При упорядочении, задаваемом <', наименьшим элементом будет 100. В самом деле:
F(100) = F(F(100+11)) = F(F(111)) = F(101)=91;
Так как n<100, то мы должны иметь
F(n) = F(F(n+11)).
Если (n+11) ∈ M, то n+11 <' n (другими словами, n < n+11 ≤ 100).
Теперь воспользуемся индуктивным определением и заключаем, что
F(n) = F(F(n+11)) = F(91).
Если (n+11) ∈ M, то n+11 ≤ 100, или n ≤ 89, но в этом случае 91 <' n (т.е. n < 91), и опять можно воспользоваться предположением индукции:
F(n) = F(F(n+11)) = F(91) = 91.
Если (n+11) ∉ M, то предположением индукции для F(F(n+11)) уже пользоваться нельзя. Однако, в этом случае известно, что n+11>100, и поэтому имеем
F(n) = F(F(n+11)) = F(n+11-10)= F(n+1).
Теперь (n+1) ∈ M, ибо n<100, и, следовательно, n+1 ≤ 100. Кроме того, n+1 <' n (другими словами, n < n+1 ≤ 100), и, применяя предположение индукции, получаем
F(n) = F(F(n+11)) = F((n+11)-10) = F(n+1) = 91,
На следующем шаге мы закончим изучение этого вопроса.
