Вполне упорядоченные множества

Выясните, какие из следующих множеств являются вполне упорядоченными множествами: (а) множество всех целых чисел; (б) множество всех натуральных чисел; (в) множество всех рациональных чисел; (г) множество всех неотрицательных рациональных чисел.
Превратится ли множество N во вполне упорядоченное множество, если отношение порядка ввести следующим образом: (а) (n,m) ∈ p, если n и m взаимно просты; (б) (n,m) ∈ p, если n является делителем m; (в) (n,m) ∈ p, если n=m²; (г) (n,m) ∈ p, если n<m; (д) (n,m) ∈ p, если n≤ m.

Семантика индуктивных определений: вычисление через расширение

1.Опишите процесс вычисления значения данной функции при заданных значениях аргументов:
(a) F: N × N → N,

(1) F(1,0); (2) F(0,2); (3) F(3,4).
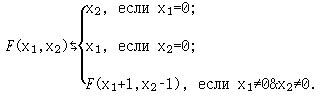
(б)

(1) G(0); (2) G(1); (3) G(2); (4) G(3).
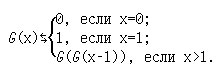
(в) функция Аккермана A: N × N → N,

(1) A(0,0); (2) A(1,0); (3) A(1,2); (4) A(2,1).

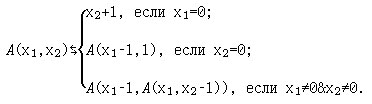
Для однозначности в любой из моментов вычислений первым вычисляйте самое левое и самое внутреннее обращение к функции A(), все аргументы которой уже не содержат обращения к функции A();
(г) W(α) ⇔ Tail(Reverse(α)),

(1) W(abaa); (2) W(ab); (3) W(bac).

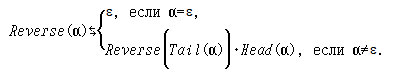
Будет ли определён результат вычисления функции W(α) при α = ε?
(д) S(α,x,β) ⇔ Subst (Head(α)+Tail(Tail(α)),x,β),

(1) S(клок,к,кол); (2) S(алгоритм,а,ал).

Определите область определения и область значения функции S.

1₁. [1, с.198]. Найдите f(1), f(2), f(3), f(4) для приведённых ниже рекурсивных функций:

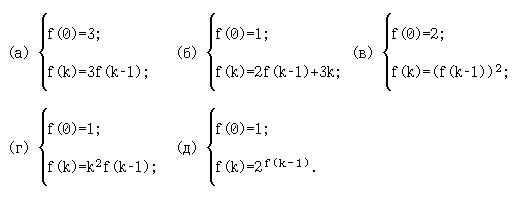
1₂. [1, с.198]. Найдите f(1), f(2), f(3), f(4) для следующих рекурсивных функций:

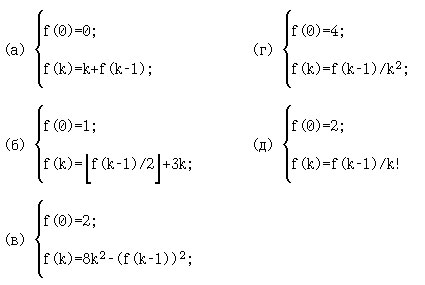
1₃. [1, с.198]. Найдите f(2), f(3), f(4) и f(5) для следующих рекурсивных функций:

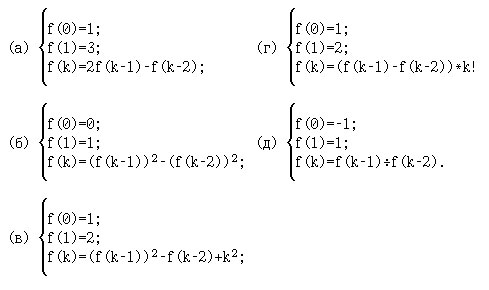
1₄. [1, с.198]. Найдите f(2), f(3), f(4) и f(5) для следующих рекурсивных функций:

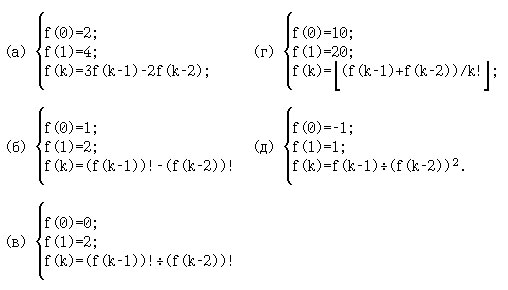
2. Определите, является ли заданная функция предикатом:

Здесь 0 и 1 - буквы некоторого алфавита.

⁽¹⁾Андерсон Дж. А. Дискретная математика и комбинаторика. - М.: Издательский дом "Вильямс", 2003. - 960 с.

На следующем шаге мы продолжим перечень заданий.

Предыдущий шаг Содержание Следующий шаг