Шаг 12.
Основы языка Haskell. Индуктивные определения операций и предикатов,... . Задания для самостоятельного решения (продолжение)

    На этом шаге мы продолжим перечень заданий для самостоятельного решения.

    Продолжим знакомство с перечнем заданий.

Определение семантики индуктивно заданной функции

    3. Определите семантику следующих функций:
(a) Sec: A*→ A*,

(б) Rep: A*×A→ A*,

(в) Sub: A*×A×A*7→ A*, 
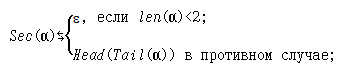
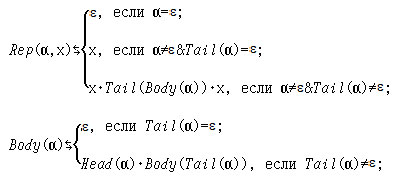
  Sub(α,x,β) ⇔ Substr (Reverse(α),x,Reverse(β))
Напишите данное определение более рациональным способом;
(г) Q: A×A*→ A+,

(д) Kol: A×A*7→ N,

    4. Дана последовательность значений функции от различных аргументов. Определите семантику функции и напишите её индуктивное определение: 

   (a) F1: N → N
        F1(1)=1;         
        F1(2)=1+1=2; 
        F1(3)=2+1=3; 
        F1(4)=3+1=4;... 

   (б) F2: N → N
        F2(1)=1;
        F2(2)=1;
        F2(3)=2;
        F2(4)=3;
        F2(5)=5;
        F2(6)=8;...

   (в) Third: A*→ A*
        Third(ε)=ε;
        Third(a)=ε;
        Third(bc)=ε;
        Third(cba)=a;
        Third(abdcea)=d;
        Third(cebfd)=b;...

   (г) Wrd3: A*→ A*
        Wrd3(ε)=ε;
        Wrd3(c)=ε;
        Wrd3(ab)=ε;
        Wrd3(cab)=b;
        Wrd3(abcdef)=cf;...

    41. [1, с.199]
Найдите явные выражения для f(n), исключив рекурсию из следующих определений:

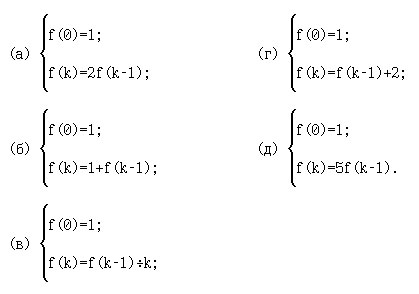
    42. [1, с.199]
Найдите явные выражения для f(n), исключив рекурсию из следующих определений:

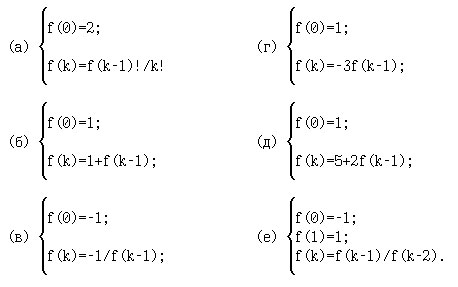
    5. Допишите индуктивное определение:
(а) предиката Compare: A+→ B2, устанавливающего тот факт, что одинаковые буквы стоят на нечётных местах в исходном слове:

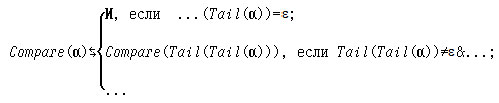
(б) функции Delete: A×A*→ A*, в результате применения которой к слову получается слово, из которого вычеркнули первое вхождение данной буквы (если таковая имеется в данном слове):

(в) функции St: A×A*→ N, являющейся степенью слова α относительно буквы x:

    6. ([2])
Что вычисляет следующая функция действительного аргумента (D - оператор дифференцирования):

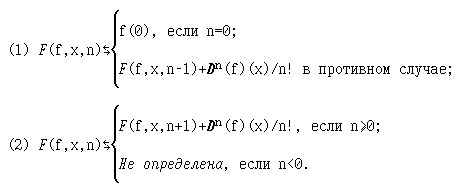
    7. (По [1, с.199-200])
Докажите, что формула для an удовлетворяет соответствующему рекурсивному определению:

Здесь  0 и 1 - буквы некоторого алфавита.
(1)Андерсон Дж. А. Дискретная математика и комбинаторика. - М.: Издательский дом "Вильямс", 2003. - 960 с.
(2)Непейвода Н.Н. Прикладная логика. - Ижевск: Изд-во Удмуртского ун-та, 1997. - 385 с.

    На следующем шаге мы закончим изучение этого вопроса.




Предыдущий шаг Содержание Следующий шаг