Шаг 13.
Основы языка Haskell. Индуктивные определения операций и предикатов,... . Задания для самостоятельного решения (окончание)

    На этом шаге мы закончим перечисление заданий для самостоятельного решения.

    Мы заканчиваем публикацию заданий для самостоятельного решения.

Построение индуктивных определений (простые задачи)

  1. Напишите индуктивное определение функции, вычисляющей модуль разности двух целых неотрицательных чисел.
  2. Напишите индуктивное определение функции, вычисляющей n-ю степень числа x, x∈N\{0}, n∈N.
  3. Напишите индуктивное определение предиката, устанавливающего, что слово состоит не менее, чем из m букв, m∈N.
  4. Напишите индуктивное определение функции, меняющей местами первую и последнюю буквы заданного непустого слова.
  5. Напишите индуктивное определение предиката, устанавливающего тот факт, что заданное слово является палиндромом.
  6. Напишите индуктивное определение функции, конструирующей слово, содержащее k букв a.
  7. Напишите индуктивное определение функции, учетверяющей каждую букву заданного слова.
  8. Напишите индуктивное определение функции, вычёркивающей из заданного слова буквы, расположенные: (1) на чётных местах; (2) на нечётных местах.
  9. Напишите индуктивное определение функции, производящей замену всех букв исходного слова на данную букву x∈A.
  10. Напишите индуктивное определение функции, производящей замену всех букв слова, стоящих на чётных местах, на заданную букву.
  11. Напишите индуктивное определение функции, которая в заданном слове заменяет все вхождения буквы x на букву y и наоборот.
  12. Напишите индуктивное определение функции, производящей перестановку каждой буквы заданного слова, расположенной на нечётном месте, с соседней справа буквой (если она есть).
  13. Напишите индуктивное определение функции, которая возвращает "центральную" букву слова.
  14. Напишите индуктивное определение предиката, устанавливающего тот факт, что в написании слова  α∈A+ использовалась только одна буква алфавита  A.
  15. Напишите индуктивное определение предиката, устанавливающего тот факт, что заданная буква имеет хотя бы одно вхождение в заданное слово.
  16. Приведите индуктивное определение функции, вычеркивающей из слова  α те буквы, которые встречаются в нём ровно n раз.
  17. Приведите индуктивное определение предиката, устанавливающего тот факт, что слово α: (1) является началом слова β; (2) является концом слова β; (3) не имеет вхождений в слово β.
  18. Приведите индуктивное определение функции, значением которой является конец слова α, началом которого является слово β.

Построение индуктивных определений (сложные задачи)

    1*. Приведите индуктивное определение:
(1) первого вхождения слова α в слово β;
(2) последнего вхождения слова α в слово β;
(3) k-го вхождения однобуквенного слова α в слово β для любого натурального k;
(4) k-го (k∈N\{0}) вхождения слова α в слово β для случая, когда все вхождения не имеют общих вхождений букв алфавита;
(5) k-го вхождения слова α в слово β для любого натурального k.

    2*. Приведите индуктивное определение операции подстановки:
(1) в слово α вместо слова γ слова β;
(1) в слово α вместо k-го вхождения слова γ слова β для любого натурального k.

    3*. Приведите индуктивное определение количества вхождений:
(1) слова γ в слово α;
(1) слова γ в слово α для случая, когда все вхождения не имеют общих вхождений букв алфавита.

    4*. Найдите ошибку, допущенную в следующем индуктивном определении k-го вхождения слова α в слово β для любого натурального k:

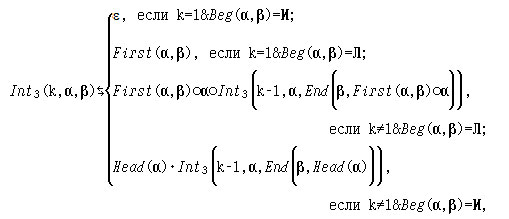
где функция First(α,β) определяет первое вхождение слова α в слово β; функция End(α,β) определяет конец слова α, началом которого является слово β; функция Beg(α,β) определяет, является ли слово α началом слова β.

    1. Определите семантику и докажите правильность индуктивного определения функции G: N\{0} → N\{0},

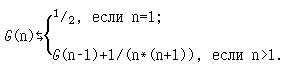
    2. Докажите правильность индуктивного определения операции приписывания слова к слову °: A*×A*→  A*:

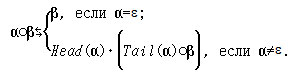
    3. Докажите правильность индуктивного определения операции "обращение слова" Reverse: A*→  A*:

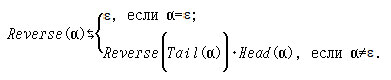
    4. Рассмотрим следующее индуктивное определение (n - натуральное число), записанное на языке структурированных программ: 

   F(n) ⇔ IF n=1
          THEN 1
          ELSE OTHERWISE n*F(n-1).
Определите семантику функции F. Докажите правильность догадки.

    5. Рассмотрим следующее индуктивное определение (n - натуральное число):

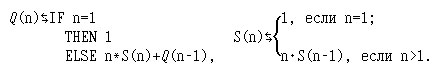
Определите семантику функции Q. Докажите правильность определения функции Q.

    6. Рассмотрим следующую программу на языке структурированных программ, применимую для неотрицательных целых n: 

   F(n) ⇔ IF n=0
          THEN 0
          ELSE OTHERWISE F(F(n-1)).
Перепишите данную программу на язык программирования LISP и докажите, что F(n)=0 для любого неотрицательного целого числа n.

    7. Определите семантику, перепишите на язык структурированных программ и докажите правильность следующей программы: 

   (DEFUN Reverse1 (LAMBDA (L)
     (COND ( (NULL L) NIL )
           ( (AND (EQ (LENGTH L) 1) (ATOM (CAR L))) L )
           (  T  (APPEND (Reverse1 (CDR L))
                         (CONS (Reverse1 (CAR L)) NIL)) ))
   ))

    8. Рассмотрим рекурсивную программу Subs(X1,X2,L), применимую к любым двум атомам X1, X2 и любому списку L: 

   Subs(X1,X2,L) ⇔ IF L=NIL
                  THEN NIL
                  ELSE IF CAR(L)=X2
                        THEN CONS(X1,Subs(X1,X2,CDR(L)))
                        ELSE IF ATOM(CAR(L))
                            THEN CONS(CAR(L),Subs(X1,X2,CDR(L)))
                            ELSE OTHERWISE CONS(Subs(X1,X2,CAR(L)),
                                                Subs(X1,X2,CDR(L)))
Перепишите данную программу на язык программирования LISP и докажите, что в этом случае Subs(X1,X2,L) есть список, полученный из L путём подстановки X1 вместо каждого вхождения элемента X2 в L. Например, SUBS(B C (A B C (A (C))))=(A B B (A (B))).

    9. Рассмотрим индуктивное определение функции F(n∈Z):

Докажите, что для всех целых n

10. Пусть А(х1,х2) - функция Аккермана. Докажите, что

для всех неотрицательных целых чисел х1 и х2.

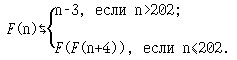
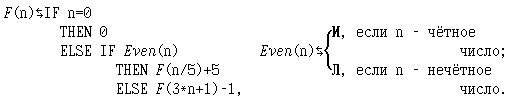
    11. Рассмотрим следующее индуктивное определение (n∈Z):

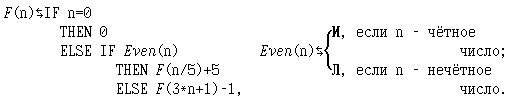
Через n/5 обозначается частное от целочисленного деления n на 5.

    Докажите, что для всех неотрицательных целых чисел n вычисление значения функции заканчивается.

    12. Рассмотрим следующее индуктивное определение (х1 и х2 - неотрицательные целые числа): 

   F(х1,х2) ⇔ IF х 41 0=0
              THEN 0
              ELSE IF х2=0
                     THEN F(х1-1,х2+1)
                     ELSE F(F(х1-1,х2),F(х1,хх2-1)).
Определите семантику функции F(х1,х2). Докажите правильность догадки.

    13. Рассмотрим рекурсивное определение (х1 и х2 - неотрицательные целые числа, удовлетворяющие условиям 0 ≤ х1 ≤ х2 и 0<х2): 

   F(х1,х2) ⇔ IF х1=0
              THEN х2
              ELSE IF х1≤х2-х1
                     THEN F(х1,х2-х1)
                     ELSE F(х2-х1,х1).
Докажите, что для любых целых х1 и х2 при условии 0 ≤ х1 ≤ х2 и 0<х2 
   F(х1,х2)=GCD(х1,х2),
где GCD - наибольший общий делитель х1 и х2.

    При доказательстве используйте тот факт, что по определению для любых рассмотренных выше х1 и х2: 

   GCD(х1,х2)=GCD(х1,х2-х1)=GCD(х2-х1,х1).

    14. Докажите правильность следующей программы, написанной на языке функционального программирования LISP: 

   (DEFUN F (LAMBDA (N)
       (COND ( (EQ N 1) 1 )
             (  T  (+ N (F (- N 1))) ))
   ))
Предполагается, что F(n)=n(n+1)/2 для любого натурального n.

    Со следующего шага мы начнем знакомиться с языком программирования Haskell.




Предыдущий шаг Содержание Следующий шаг