На этом шаге мы рассмотрим еще один пример трансформации функций.
Рассмотрим еще один пример.
Пример 2 ([1, с.83]).
Рассмотрим следующие рекуррентные соотношения:
f(0)=0, f(1)=1, f(n)=f(n-1)+f(n-2).
Преобразуем эту рекурсию высшего порядка в простую рекурсию.
Рассмотрим новую функцию, значением которой является пара:
g(n)=(f(n+1),f(n)),
g(0)=(f(1),f(0))=(1,1).
Определим рекуррентные соотношения для функции g():
g(n+1)=(f(n+2),f(n+1))=(f(n+1)+f(n),f(n+1)) =>
=> g(n+1)=(u+v,u)
where (u,v)=(f(n+1),f(n))=g(n).
Остаётся преобразовать выражение для функции f():
f(n+2)=f(n)+f(n+1) => f(n+2)=u+v
where (u,v)=(f(n+1),f(n))=g(n).
Таким образом, получена взаимная рекурсия:
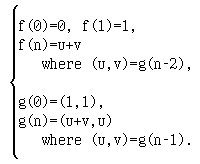
Поработаем с демонстрационными примерами.
-- Демонстрация применения трансформации программ на при- -- мере функции, вычисляющей n-ое число Фибоначчи с помо- -- щью рекуррентных соотношений: -- -- f(0)=1, f(1)=1, -- -- f(x)=f(x-1)+f(x-2) -- ********************* fib:: Integer -> Integer fib 0 = 1 fib 1 = 1 fib (n+1) = fib n + fib (n-1) ----------------------------- -- Результат трансформации -------------------------- f 0 = 1 f 1 = 1 f n = u+v where (u,v)=g (n-2) ---------------------- g 0 = (1,1) g n = (u+v,u) where (u,v)=g (n-1) -- ************************************************* -- Функция, возвращающая аргумент функции Фибоначчи, -- для которого значение функции меньше 4294967295 ----------------------------------------------------- len = fst $ last $ takeWhile (\(x,y) -> y<4294967295) (map (\x -> (x,f x)) [1..]) -- ***************************************************** -- Неудачные тестовые примеры: ------------------------------ test1 = fib 11 == 144 && fib 23 == 46368 --------------------------- test2 = f 11 == 144 && f 23 == 46368 && f 30 == 1346269 ----------------------------- test3 = f 3000+f 3001==f 3002
(1)Сергиевский Г.М., Волчёнков Н.Г. Функциональное и логическое программирование. - М.: Издательский центр "Академия", 2010. - 320 с.
На следующем шаге мы рассмотрим некоторые итерационные методы решения уравнений.
