На этом шаге мы приведем задачи для самостоятельного решения.
Замечание. Найдите ошибки, описки, неточности и прочие изъяны в приведенных задачах.
1. Определение прагматики рекурсивных функций
1*. Укажите прагматику (назначение) рекурсивных функций:
(1) mult n 0 = 0
mult n m = mult n (m-1)+n
(2) russ n 1 = n
russ n m | m `mod` 2==0 = russ (n*n) (m `div` 2)
| True = n*russ (n*n) (m `div` 2)
(3) z:: Int -> Int -> Int
z p n | n<p = 0
| True = 1 + z p (n `div` p)
(4) 5* 0 f:: Int -> String
f n | n>=1000 = "M" ++ f (n-1000)
| n>=500 = "D" ++ f (n-500)
| n>=100 = "C" ++ f (n-100)
| n>=50 = "L" ++ f (n-50)
| n>=10 = "X" ++ f (n-10)
| n>=5 = "V" ++ f (n-5)
| n>=1 = "I" ++ f (n-1)
| True = ""
---------------------------------------
-- Неудачные тестовые примеры:
---------------------------------------
testF = f 12=="XII" && f 1256=="MCCLVI"
2*. Напишите программу для вычисления значения приведённой ниже функции (x,y,z ∈ N) и вычислите с её помощью F(5,0,0), F(1000,0,0).
F(x,y,z) = если x=0
то 0
иначе если y+1=x
то z
иначе F(x,y+1,z+1)
Указание (по [9, с.6]). Известный американский математик А.Чёрч (автор тезиса Чёрча), создал на подступах к теории алгоритмов λ-исчисление, являющееся теоретической моделью функционального программирования. Он безуспешно пытался выразить в языке λ-исчисления операцию вычитания единицы из натурального числа (знак операции "Sub")
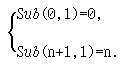
А.Чёрч уже уверился в неполноте своего исчисления, но С.Клини (тогда молодой аспирант) в 1932 г. предложил конструкцию, полностью отвечающую сути дела и приведённую нами выше.
3*. Определите прагматику функции и реализуйте её на Haskell:
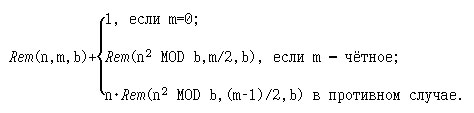
Указание. Функция Rem(n,m,b) для целых чисел n,m,b>0 вычисляет остаток от деления nm на b.
4*. Определите прагматику приведённой ниже рекурсивной функции и реализуйте её на языке Haskell:
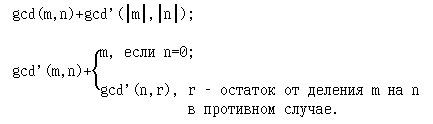
5.([1, с.209]) Определите прагматику функции Rom(n) и реализуйте её на языке Haskell ("*" - операция приписывания буквы слева к слову):

Указание. Функция Rom(n) осуществляет перевод натурального числа в его "римскую запись" и реализует первоначальную римскую систему счисления. Такие сокращенные способы записи, как, например, IV вместо IIII вошли в употребление лишь в начале XVI в.
2. Рекурсивные функции на числовых структурах
1*. Напишите функцию, вычисляющую факториал натурального числа с помощью рекурсии по аргументам.
2*. Напишите функцию, вычисляющую факториал натурального числа с помощью рекурсии по значению.
3*. Напишите функцию, вычисляющую число сочетаний из n элементов по m.
4*. Напишите функцию, вычисляющую значение функции при n,m ∈ N:
(1) F(n)=4n; (2) F(n)=nn; (3) F(m,n)=mn.
5*. [1] Напишите рекурсивную функцию, моделирующую операцию сложения натуральных чисел с помощью тождества
(a+1)+(b-1)=a+b.
6. ([2]) Напишите программу, вычисляющую значение следующих функций при значениях n ∈ N \ {0}:
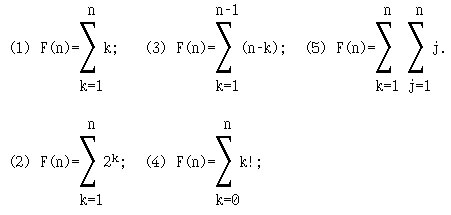
7*. Напишите функцию, вычисляющую значение функции n!!.
8*. [1] Напишите функцию, определяющую для натурального числа n ≥ 1 единственное натуральное число ld(n), такое, что
2ld(n)-1≤ n < 2ld(n), ld(1)=1.
Указание. Для тестирования выразите функцию ld(n) из уравнения
n=2ld(n)-1 .
9*. [3, с.345] Напишите программу на языке Haskell для вычисления значения функции, заданной рекуррентными соотношениями:
D(0)=1, D(n)=(D(n-1)2)+1.
Указание. Для тестирования воспользуйтесь тем, что
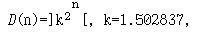
10*. Напишите рекурсивную функцию, осуществляющую перевод натуральных чисел: (а) из десятичной системы счисления в двоичную; (б) из двоичной системы счисления в десятичную.
11*. Напишите рекурсивную функцию, реализующую факторизацию натурального числа n>1, т.е. возвращающую разложение натурального числа на простые множители.
12*. Напишите программу, вычисляющую значение функции при значениях x ∈ R:
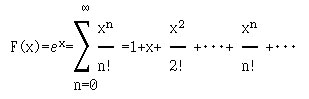
13*. [4, с.62, №7.18]) Дано целое положительное n. Найдите
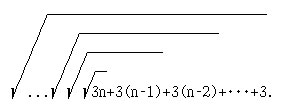
14*. [4, с.63, №7.23]) Дано целое положительное n. Найдите
1/(20+1/(21+1/.../(2n+1/2n+1)...)).
3. Сложная рекурсия на числовых структурах
1*. Напишите функцию на языке Haskell, заданную так:

Указание. Для тестирования воспользуйтесь тем, что n ∈ Z

2*. Напишите на языке Haskell функцию "191-МакКарти", заданную следующим образом:
F(n)=If n>100
then n-10
else F(F(F(n+21)))
3. Напишите функцию на языке Haskell, реализующую вычисление значения функции Аккермана:
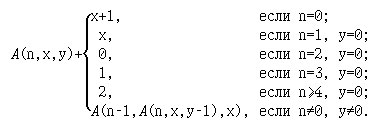
Указание. Для тестирования воспользуйтесь тестовыми примерами:
A(0,x,y)=x+1, A(1,x,y)=x+y, A(2,x,y)=x * y, A(3,x,y)=xy.
4. ([4, с.77, №8.18]) Напишите программу на языке Haskell для вычисления значения заданной функции f(x,y) при заданных x, y:
f(0,y)=y, если y ∈ N; f(x,0)=x, если x ∈ N; f(x,x)=f(x-1,x-1)+1, если x>0; f(y,y)=f(y+1,y+1)-1, если y<0; f(x,y)=f(x,x)+f(y,y), если x ≠ y.
5. ([5, с.199-200]) Напишите функцию, вычисляющую значения an по заданному рекурсивному определению:

Указание. Для тестирования воспользуйтесь соотношениями:
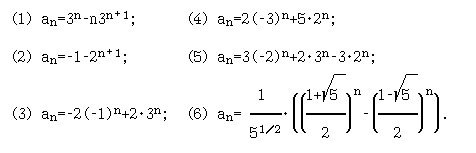
6. [4, с.34, №3.20]) Что вычисляет данная программа?
F(x,y)= if y=0 then 0 else F(F(x,y),F(y,x)) fi
7*. [4, с.191, №16.16] Определим функцию f(x) для целого неотрицательного аргумента x:
f(0)=0, f(1)=1, f(2n)=n, f(2n+1)=f(n)+f(n+1).
4. "Проверка" математических результатов
1. Напишите функции для вычисления (x,y ∈ R):
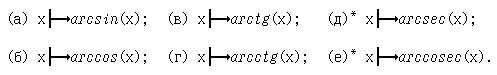
2*. "Проверьте", используя рекурсию, следующее равенство
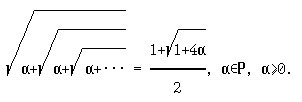
Указание. В качестве тестовых примеров для проверки получения целочисленных результатов вычислений рассмотрите случаи:
α= 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132,
156, 182, 210, 240, 272, 306, 342, 380, 420, 462, 992,
test = filter (\x -> denominator (snd x)==1)
(map (\x -> (x,toRational ((1+sqrt (1+4*x))/2)))
[2..1000])
3. [6, с.31] "Проверьте" результат С.Рамануджана, используя рекурсию:
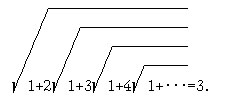
4. [6, с.31] "Проверьте" результат С.Рамануджана, используя рекурсию:
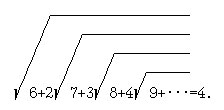
5. ([68, с.32]) "Проверьте" результат С.Рамануджана, используя рекурсию:
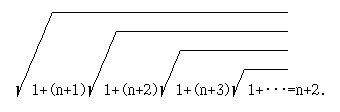
6. [6, с.31] "Проверьте" результат С.Рамануджана, используя рекурсию:
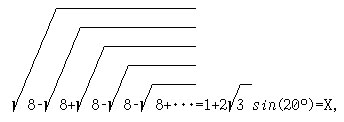
Выведите уравнение, корнем которого является X.
Указание. [6, с.32-34]. Приведём следующие выкладки:
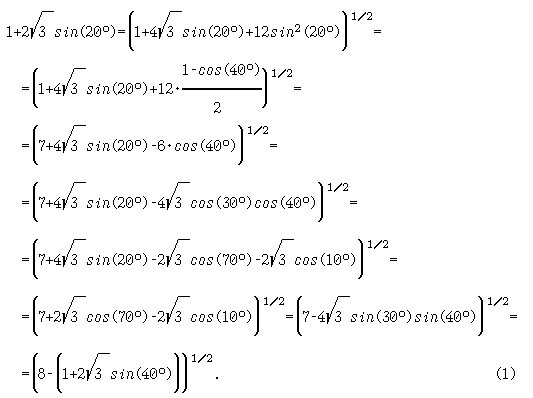
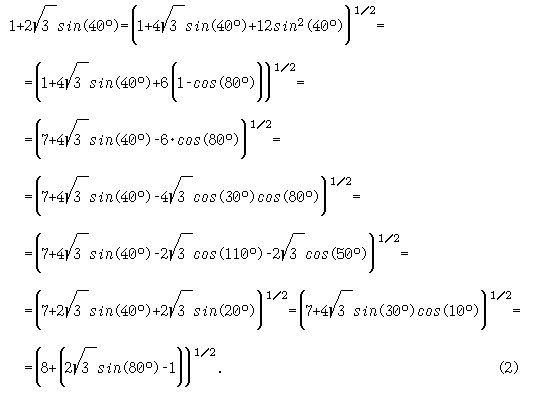
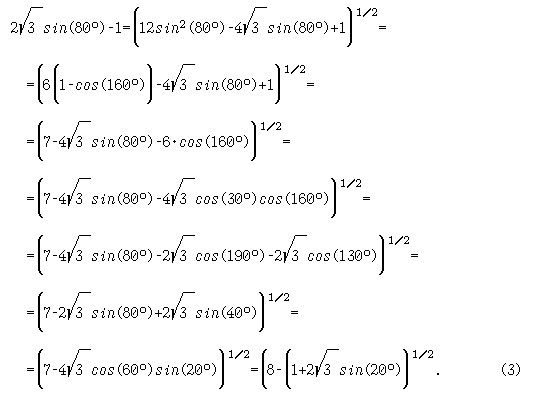
Подстановка друг в друга (1), (2) и (3) приводит к равенству:
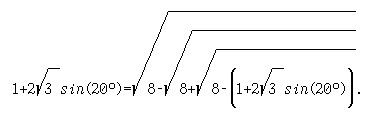
Искомая формула может быть получена отсюда итерированием (повторной подстановкой).
7. [6, с.31] "Проверьте" результат С.Рамануджана, используя рекурсию:
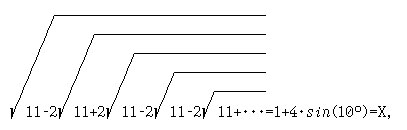
Выведите уравнение, корнем которого является X.
8. [6, с.31] "Проверьте" результат С.Рамануджана, используя рекурсию:
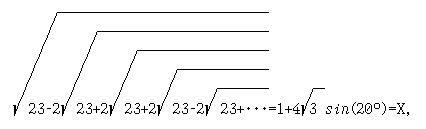
Выведите уравнение, корнем которого является X.
9. "Проверьте", используя рекурсию, следующий результат Ф.Виета (1540-1603) (разумеется, Ф.Виет не доказывает сходимости полученного бесконечного произведения, будучи интуитивно уверенным в справедливости своего предельного утверждения):
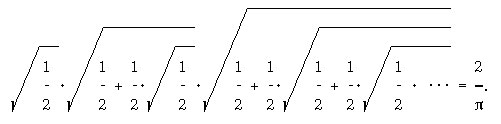
Замечание ([7, с.133]). "Любопытная формула! - комментирует её Ф.Кыпман, - она походит на фантастический лабиринт с тысячами комнат, в которых прячется число π. Если мы его ищем под первым радикалом, то обнаруживаем дверь, ведущую ко второму радикалу, через которую оно удрало от нас. Если преследовать его дальше, оно находит убежище под третьим радикалом, как бы охраняемым дробью 1/2, и так далее".
10. "Проверьте", используя рекурсию:

11. ([7, с.136]) "Проверьте", используя рекурсию, результат У.Броункера (1620-1684), полученный в 1665 г., и результат Л.Эйлера (1707-1783):
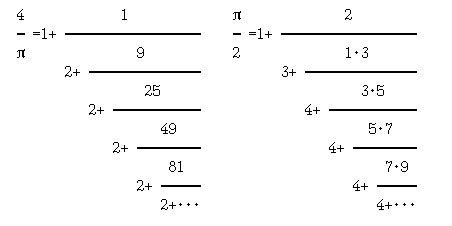
12. [8, с.82] Представление функции "тангенс" в виде цепной дроби было опубликовано немецким математиком Й.Х.Ламбертом (1770)
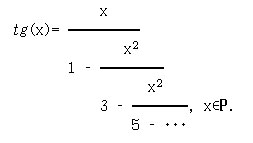
Определите функцию tan x k, которая вычисляет приближение к тангенсу на основе формулы Ламберта.
Аргумент k указывает количество шагов вычислений.
13. ([7, с.136]) Известно представление функции "арктангенс" в виде цепной дроби:
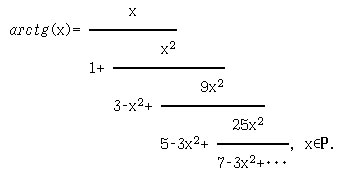
Определите функцию arctan x k, которая вычисляет приближение к значению функции "арктангенс".
Аргумент k указывает количество шагов вычислений.
14. ([7, с.60-61]) Реализуйте, используя рекурсию, алгоритм Дж.Борвейна и П.Борвейна [1988] для расчёта десятичных знаков числа π, который приведён ниже. Члены последовательности a0, a1, a2,... вычисляются по рекуррентным формулам:
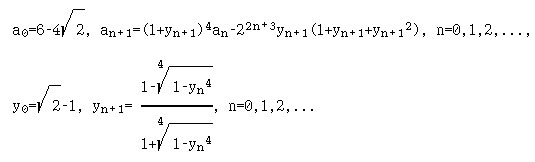
По мере увеличения номера шага n величина 1/an очень быстро приближается к π (уже при n=4 количество верных знаков равно 694).
Указание. Этот алгоритм имеет фантастическую эффективность: каждый новый шаг выполнения алгоритма уточняет количество верных цифр в разложении числа π более, чем вчетверо.
Авторы алгоритма утверждают, что у истоков их открытия лежали идеи индийского математика С.Рамануджана (1887-1920).
(1)Бауэр Ф.Л., Гооз Г. Информатика. Вводный курс. Ч.1. - М.: Мир, 1990. - 336 с.; Ч.2. - М.: Мир, 1990. - 423 с.
(2)Душкин Р.В. Функциональное программирование на языке Haskell. - М.: ДМК Пресс, 2007. - 608 с.
(3)Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. Т.1. Синтаксический анализ. - М.: Мир, 1978. - 614 с.
(4)Анисимов А.Е., Пупышев В.В. Сборник заданий по основаниям программирования. - М.: Интернет-Университет Информационных Технологий; БИНОМ. Лаборатория знаний, 2006. - 248 с.
(5)Андерсон Дж. А. Дискретная математика и комбинаторика. - М.: Издательский дом "Вильямс", 2003. - 960 с.
(6)Левин В.И. Рамануджвн - математический гений Индии. - М.: Знание, 1968. - 48 с.
(7)Жуков А.В. Вездесущее число "пи". - М.: Едиториал УРСС, 2004. - 216 с.
(8)Абельсон Х., Сассман Дж. Структура и интерпретация компьютерных программ - язык Lisp. - М.: Добросвет, 2006 - 608 с.
(9)Хендерсон П. Функциональное программирование. Применение и реализация. М.: Мир, 1983. - 349 с.
Со следующего шага мы начнем рассматривать списки.
