На этом шаге мы введем указанные понятия.

Определение [1, с.373] (содержательное).

Будем говорить, что два бинарных дерева T₁ и T₂ подобны, если они имеют одинаковую структуру (другими словами, подобие бинарных деревьев означает, что графические изображения деревьев T₁ и T₂ имеют одинаковую "конфигурацию").

Определение [1, с.373] (индуктивное).

Подобными бинарными деревьями называются бинарные деревья, которые:

(1) либо оба пусты;
(2) либо оба непусты, а их левые и правые поддеревья соответственно подобны.

Обозначим Info(u) информацию, содержащуюся в вершине u.

Определение [1, с.373] (содержательное).

Будем говорить, что бинарные деревья T₁ и T₂ эквивалентны, если:

(1) они подобны;
(2) соответствующие вершины содержат одинаковую информацию.

Определение [1, с.352] (формальное).

Эквивалентными бинарными деревьями T₁ и T₂ называются бинарные деревья, которые:

(1) либо оба пусты;
(2) либо оба непусты и Info(Корень (T)) = Info(Корень (T')), а их левые и правые поддеревья соответственно эквивалентны.

Пример. Рассмотрим четыре бинарных дерева:

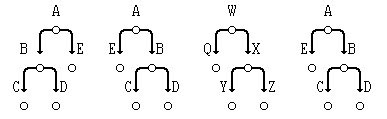
Рис.1. Бинарные деревья

Первые два из них - не подобны; второе, третье и четвёртое деревья - подобны; второе и четвертое - эквивалентны.

Определение (содержательное).: Изоморфными бинарными деревьями называются два бинарных дерева, которые можно отобразить одно в другое, изменив порядок сыновей узлов одного из них.

⁽¹⁾Кнут Д.Э. Искусство программирования, том 1. Основные алгоритмы. - М.: Издательский дом "Вильямс", 2000. - 720 с.

На следующем шаге мы рассмотрим бинарное дерево поиска.

Предыдущий шаг Содержание Следующий шаг