На этом шаге мы рассмотрим это понятие.
- Определение [1, с.356] (содержательное).
- Бинарное дерево - это конечное множество элементов (называемых вершинами или узлами), которое либо пусто (!), либо состоит из корня (некоторая выделенная вершина), связанного с двумя различными бинарными деревьями, называемыми левым и правым поддеревом корня.
Важно отметить, что бинарное дерево не является частным случаем дерева, определённого на 130 шаге:
- (1) бинарное дерево может быть пустым, а "обычное" дерево - нет;
- (2) бинарное дерево представляет собой упорядоченное дерево (см. в определении понятия "бинарное дерево" слова "... с двумя различными бинарными деревьями..."), у которого в каждую вершину, отличную от корня, входит только одна дуга, а выходит не более двух. При этом для каждой входящей дуги известно, является ли она правой или левой.
Следовательно, при работе с бинарными деревьями нельзя забывать об обязательном прилагательном "бинарный", чтобы не путать их с "обычными" деревьями.
Изобразим несколько бинарных деревьев:
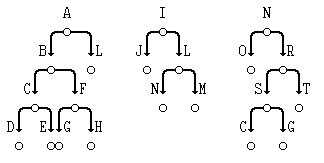
Рис.1. Примеры бинарных деревьев
Каждая вершина бинарного дерева, отличная от корня, может рассматриваться как корень бинарного поддерева с вершинами, достижимыми из неё.
(1)Кнут Д.Э. Искусство программирования, том 1. Основные алгоритмы. - М.: Издательский дом "Вильямс", 2000. - 720 с.
На следующем шаге мы рассмотрим подобные, эквивалентные и изоморфные бинарные деревья.
