На этом шаге мы рассмотрим различные варианты этого алгоритма.
Будем исходить из того, что:
- (1) новый узел всегда добавляется в бинарное дерево как лист с двумя потомками - чёрными NIL-узлами;
- (2) корень красно-чёрного дерева должен быть чёрным.
Теперь для сохранения свойства чёрного узла будем включать красный узел в лист, а затем исправлять нарушение свойства красного узла (если оно возникнет).
Процесс исправления нарушений свойств красно-чёрного дерева будет повторяться по пути, ведущему от нового узла к корню дерева.
Рассмотрим случаи, которые могут возникнуть, если отец включаемого узла S имеет красный цвет.
1. Ситуация "красный отец, чёрный дядя ".
(а) D - левый потомок G; S - левый потомок D:
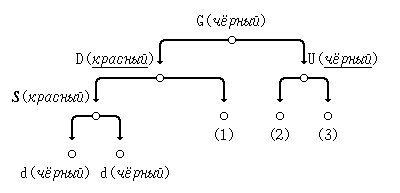
Исправим нарушение свойства красного узла так:
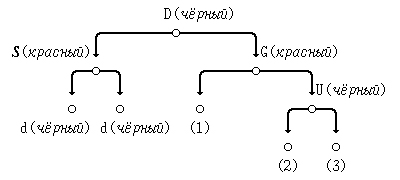
- (1) перекрасим узел D в чёрный цвет, в G - в красный;
- (2) выполним правую ротацию узла D; в результате G становится дочерним узлом узла D.
(б) D - левый потомок узла G; S - правый потомок узла D:
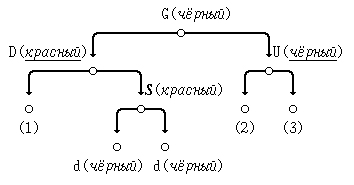
Исправим нарушение свойства красного узла так:
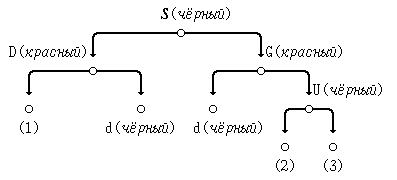
- (1) перекрасим узел S в чёрный цвет, в G - в красный;
- (2) выполним спаренный двусторонний поворот узла S (влево, затем - вправо) для размещения узла S на месте узла G.
Замечание (важное для уменьшения количества операций). Можно свести рассматриваемый случай к случаю (а):
(1) осуществив левую ротацию узла S:
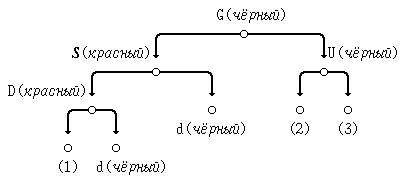
(2) поменяв местами метки вершин S и G:
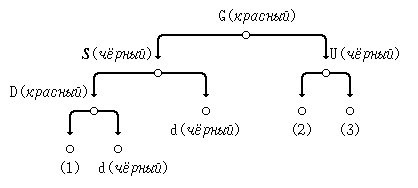
(3) выполним правую ротацию узла G:
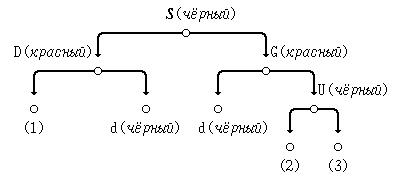
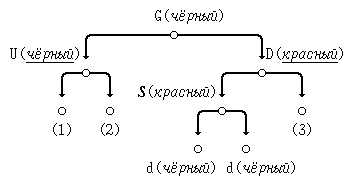
(в) зеркальное отражение случая (a): D - правый потомок G; S - правый потомок D:
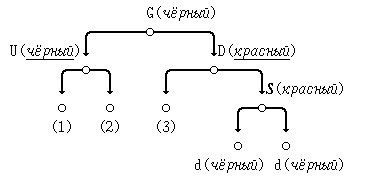
Исправим нарушение свойства красного узла так:
- (1) перекрасим узел D в чёрный цвет, в G - в красный;
- (2) выполним левую ротацию узла D на место узла G; в результате G становится дочерним узлом D.
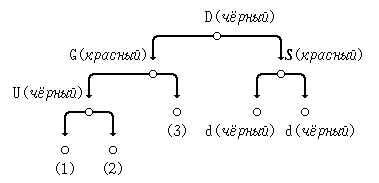
(г) зеркальное отражение случая (б): D - правый потомок G; S - левый потомок D:
Исправим нарушение свойства красного узла так:
- (1) перекрасим узел S в чёрный цвет, в G - в красный;
- (2) выполним спаренный двусторонний поворот узла S (вправо, затем - влево) для размещения узла S на месте узла G.
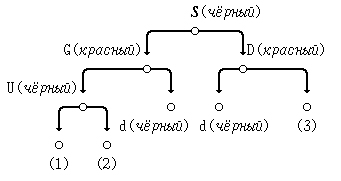
Замечание (важное для уменьшения количества операций). Можно свести рассматриваемый случай к случаю (в):
- (1) осуществив правую ротацию узла S;
- (2) поменяв местами метки вершин S и D;
- (3) выполнив левую ротацию узла G.
На следующем шаге мы закончим рассмотрение этого вопроса.
