На этом шаге мы закончим изучение этого вопроса.
2. Ситуация "красный отец, красный дядя".
(а) D - левый потомок G; S - левый потомок D:
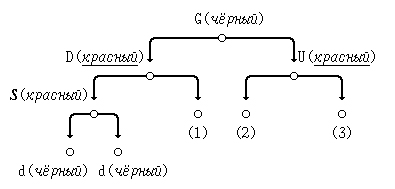
Исправим нарушение свойства красного узла с помощью перекрашивания узлов D и U в чёрный цвет, а G - в красный:
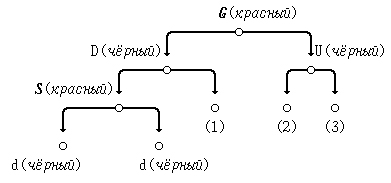
Конфликтная ситуация (а) исправлена, однако предком вершины G может оказаться красный узел. Поэтому в рассмотрение "нарушителя" свойств красно-чёрных деревьев поступает вершина G.
Процесс балансировки конструируемого дерева продолжается.
Действия алгоритма повторяются.
Рассмотрим оставшиеся случаи, в которых исправление нарушения свойств красно-чёрного дерева одинаково.
(б) D - левый потомок узла G; S - правый потомок узла D:
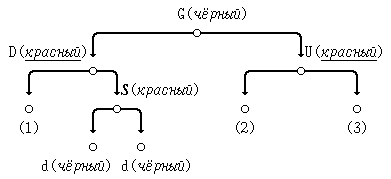
В этом случае перекрасим узлы D и U в чёрный цвет, а узел G - в красный.
(в) зеркальное отражение случая (а): D - правый потомок узла G; S - правый потомок узла D:
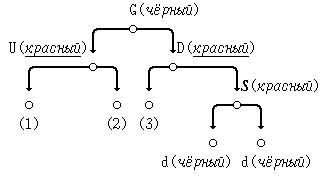
В этом случае перекрасим узлы U и D в чёрный цвет, а узел G - в красный.
(г) зеркальное отражение случая (б): D - правый потомок узла G; S - левый потомок узла D:
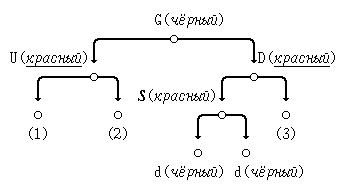
В этом случае перекрасим узлы U и D в чёрный цвет, а узел G - в красный.
Замечание (важное). Алгоритм включения в красно-чёрное дерево имеет временную сложность:
O(log2n).
На следующем шаге мы приведем этот же алгоритм на псевдокоде.
