На этом шаге мы рассмотрим назначение и структуру матрицы иницидентности.
- Определение (классический способ представления графов) [1, с.84-85].
- Матрицей инцидентности называется матрица A с N строками, соответствующими вершинам, и M столбцами, соответствующими рёбрам.
В случае неориентированного графа столбец, соответствующий ребру {x,y}, содержит 1 в строках, соответствующих x и y и 0 - в остальных строках.
Для ориентированного графа столбец соответствующий дуге <x,y>, принадлежащей E, содержит -1 в строке, соответствующей вершине x, 1 - в строке, соответствующей вершине y, и 0 - во всех остальных строках (петлю, т.е. дугу вида <x,x>, удобно представлять иным значением в строке x, например, 2).
Рассмотрим два графа: (а) ориентированный граф; (б) неориентированный граф (рисунок 1).
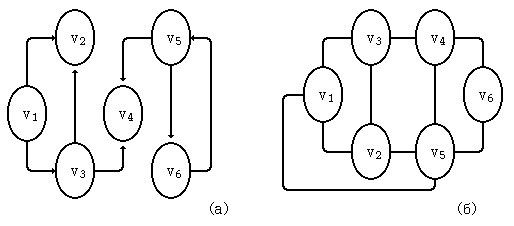
Рис.1. Графы
Матрицы инцидентности для данных графов имеют следующий вид (рисунок 2):
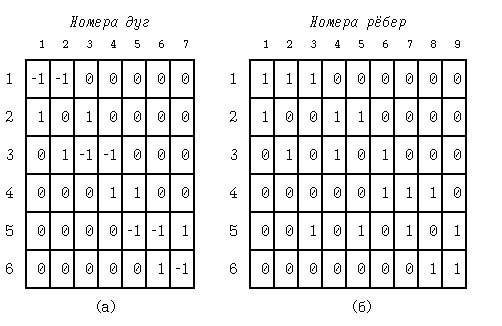
Рис.2. Матрицы инцидентности графов
Замечание.
- Никакие два столбца матрицы инцидентности не идентичны.
- Каждый столбец в матрице содержит две единицы.
- Количество единиц в i-ой строке равно степени вершины i в графе.
С алгоритмической точки зрения матрица инцидентности является, вероятно, самым худшим способом представления графа:
- (1) способ требует N × M ячеек памяти, причём большинство этих ячеек вообще занято нулями;
- (2) неудобен доступ к информации: ответ на элементарные вопросы типа "существует ли дуга <x,y>?", "к каким вершинам ведут ребра из вершины x?" требует в худшем случае перебора всех столбцов матрицы, а следовательно, M шагов.
Тем не менее, представление графов с помощью матриц смежности иногда удобно в теоретических рассуждениях; например имеют место следующая теорема [2, с.28]: графы (ориентированные графы) изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга произвольными перестановками строк и столбцов.
Также матрица инцидентности полезна при решении задач о циклах (или контурах) в теории графов.
(1)Липский В. Комбинаторика для программистов. - М.: Мир, 1988. - 213 с.
(2)Лекции по теории графов / Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. - М.: Наука, 1990. - 384 с.
На следующем шаге мы рассмотрим матрицу достижимости.
