На этом шаге мы рассмотрим Назначение и особенности матрицы достижимости.
Рассмотрим, следуя монографии [1, с. 439], степени матрицы смежностей ориентированного графа G=(V,E). Единица в i-й строке и j-м столбце матрицы смежностей A указывает на наличие дуги (vi,vj), т.е. на наличие пути длины 1 из вершины vi в вершину vj. Обозначим элементы матрицы A2 через a(2)ij. Тогда
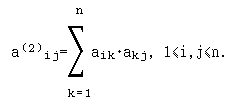
Для каждого k=1, 2, ..., n условие aik*akj=1 выполняется тогда и только тогда, когда оба элемента aik и akj равны 1, т.е. в графе имеются дуги (vi,vk) и (vk,vj). Для каждого такого k мы получаем "единичный вклад" в сумму. Наличие дуг (vi,vk) и (vk,vj), означает, что существует путь из vi в vj длины 2. Тем самым a(2)ij равно числу различных путей длины 2 из vi в vj. Аналогично диагональный элемент a(2)ii указывает число циклов длины 2 в вершине i для любого i=1, 2, ..., n.
С помощью подобной аргументации мы можем показать, что элемент в i-й строке и j-м столбце матрицы A3 задает количество путей длины 3 из вершины vi в вершину vj.
В общем случае может быть доказано следующее утверждение.
- Теорема.
- Пусть A - матрица смежностей ориентированного графа G. Элемент на пересечении i-й строки и j-го столбца матрицы An равен количеству путей длины n из i-й вершины в j-ю вершину.
Ясно, что получив матрицу Bn=A + A2+ ... + An, можно определить количество путей из vi в vj длины, меньшей или равной n.
Если бы требовалось определить, достижима ли вершина vj из вершины vi, было бы необходимо исследовать, существует ли путь любой длины из вершины vi в вершину vj. Чтобы решить этот вопрос с помощью матрицы смежностей, мы должны были бы рассмотреть все возможные Ak для k=1, 2, ...; однако этот метод не является рациональным.
Пусть G=(V,E) - ориентированный граф, содержащий n вершин.
- Определение.
- Матрица P размерности n × n, элементы которой задаются выражением
называется матрицей достижимости (путевой матрицей) графа G.
⌈ 1, если существует путь из вершины vi в вершину vj; pij ⇔ ⌊ 0, в противном случае.
Матрица достижимости лишь показывает, имеется или отсутствует по крайней мере один путь между парой вершин графа, а также имеется или отсутствует контур в любой вершине. Вместе с тем, она не определяет все пути, которые могут существовать. В этом смысле матрица достижимости не дает столь полной информации о графе, как матрица смежностей. Однако матрица достижимости важна сама по себе.
Её можно получить из матрицы Bn, положив
⌈ 1, если bij ∈ Bn и bij ≠ 0;
pij ⇔
⌊ 0, в противном случае.
Например, если
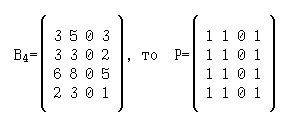
(1)Трамбле Ж., Соренсон П. Введение в структуры данных. - М.: Машиностроение, 1982. - 784 с.
На следующем шаге мы рассмотрим другие матричные представления.
