На этом шаге мы рассмотрим назначение и примеры использования этих типов.

    Алгебраические типы данных (Algebraic Data Types, ADT) позволяют выражать закрытое множество возможных подтипов, которые могут быть ассоциированными с заданным типом. Перечисления - это простейшая форма ADT.

    Представьте класс Student, который имеет три ассоциативных состояния, зависящих от статуса зачисления:

• NOT_ENROLLED (не зачислен),
• ACTIVE (зачислен) и
• GRADUATED (выпущен).

    Используя класс перечисления, о котором вы узнали в предыдущих шагах, можно смоделировать эти три состояния для класса Student следующим образом:

enum class StudentStatus {
    NOT_ENROLLED,
    ACTIVE,
    GRADUATED
}

class Student(var status: StudentStatus)

fun main(args: Array<String>) {
    val student = Student(StudentStatus.NOT_ENROLLED)
}

    Также можно написать функцию, которая выводит сообщение о статусе студента:

fun studentMessage(status: StudentStatus): String {
    return when (status) {
        StudentStatus.NOT_ENROLLED -> "Please choose a course."
    }
}

    Одно из преимуществ перечислений и других ADT в том, что компилятор может проверить, обработаны ли все возможные варианты, потому что ADT - это закрытое множество всех возможных типов. Реализация studentMessage не обрабатывает типы ACTIVE и GRADUATED, поэтому компилятор выдаст ошибку (рисунок 1).

Рис.1. Нужно добавить необходимые варианты

    Компилятор будет удовлетворен, если ко всем типам обращаются явно или они указаны в ветви else:

fun studentMessage(status: StudentStatus): String {
    return when (status) {
        StudentStatus.NOT_ENROLLED -> "Please choose a course."
        StudentStatus.ACTIVE -> "Welcome, student!"
        StudentStatus.GRADUATED -> "Congratulations!"
    }
}

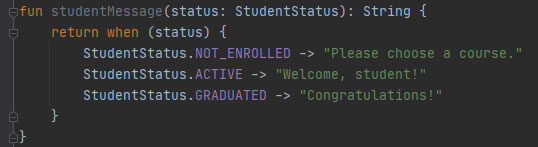
Рис.2. Варианты добавлены

    Для более сложных ADT можно использовать изолированные (sealed) классы, которые позволяют реализовать более изощренные объявления. Изолированные классы позволяют определить ADT, похожие на перечисления, но с большим контролем над подтипами.

    Например, у поступившего студента также должен быть студенческий билет. Можно добавить свойство билета в перечисление, но оно нужно только для случая ACTIVE, в остальных же случаях оно создает два нежелательных состояния null для свойства:

enum class StudentStatus {
    NOT_ENROLLED,
    ACTIVE,
    GRADUATED;
    var courseId: String? = null // Используется только для состояния ACTIVE
}

    Лучшим решением будет использование изолированного класса для моделирования состояния студента:

sealed class StudentStatus {
    object NotEnrolled : StudentStatus()
    class Active(val courseId: String) : StudentStatus()
    object Graduated : StudentStatus()
}

    Изолированный класс StudentStatus имеет ограниченное количество подклассов, которые должны быть объявлены в том же файле, что и StudentStatus. В противном случае он будет непригоден для создания подклассов. Объявление изолированного класса вместо перечисления для выражения возможных состояний студента позволяет указать ограниченный набор состояний, которые компилятор сможет проверить в операторе when (как в случае с перечислением), но дает больше контроля над объявлением подклассов.

    Ключевое слово object используется для состояний, когда студенческого билета нет, так как вариаций этих состояний не будет, а ключевое слово class используется для класса ACTIVE, потому что у него будут другие состояния, так как номер студенческого билета будет меняться от студента к студенту.

    Использование нового изолированного класса в when позволит вам прочесть номер билета courseId из класса ACTIVE через умное приведение типа:

fun main(args: Array<String>) {
    val student = Student(StudentStatus.Active("Kotlin101"))
    studentMessage(student.status)
}
fun studentMessage(status: StudentStatus): String {
    return when (status) {
        is StudentStatus.NotEnrolled -> "Please choose a course!"
        is StudentStatus.Active -> "You are enrolled in: ${status.courseId}"
        is StudentStatus.Graduated -> "Congratulations!"
    }
}

    На следующем шаге мы рассмотрим несколько заданий для самостоятельного решения.

Предыдущий шаг Содержание Следующий шаг