На этом шаге мы рассмотрим применение матрицы смежности для представления графов.
Пусть G - помеченный граф порядка N, V = {1,2,...,N}.
Лучшим способом представления графа является матрица смежности, определяемая как матрица B = [Bij] размера NxN, где Bij=1, если существует ребро, идущее из вершины i в вершину j, и Bij=0 в противном случае. Заметим, что количество единиц в строке матрицы смежности равно степени соответствующей вершины.
Нетрудно видеть, что матрица смежности неориентированного графа всегда симметрична. Для ориентированного графа это не так.
Основным преимуществом матрицы смежности является тот факт, что за один шаг можно получить ответ на вопрос "существует ли ребро из i в j?".
Недостатком же является тот факт, что независимо от количества ребер объем занятой памяти составляет NxN. На практике это неудобство можно иногда уменьшить, храня целую строку (столбец) матрицы в одном машинном слове - это возможно для малых N.
Для представления матрицы в виде S-выражения воспользуемся следующей структурой: строки матрицы определим как упорядоченные списки матричных элементов, а саму матрицу как список строк.
Приведем пример построения S-выражения, соответствующего ориентированному графу:
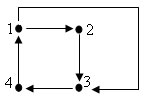
Рис.1. Ориентированный граф
Матрица S-выражение
смежности
(0 1 1 0) ( (0 1 1 0)
(0 0 1 0) (0 0 1 0)
(0 0 0 1) (0 0 0 1)
(1 0 0 0) (1 0 0 0)
)
В неориентированном графе GRAPH найдем список соседей вершины X (т.е. вершин, соединенных с ней хотя бы одним ребром), воспользовавшись представлением графа в виде матрицы смежности.
Программа.
(DEFUN NEIGHBOUR1 (LAMBDA (X GRAPH)
(VSPOM 1 (NTH X GRAPH))
))
; ------------------------ ;
(DEFUN VSPOM (LAMBDA (I LST)
(COND ( (NULL LST) NIL )
( (EQ (CAR LST) 1)
(CONS I (VSPOM (+ I 1) (CDR LST))) )
( T (VSPOM (+ I 1) (CDR LST)) )
)
))
; ---------------------- ;
(DEFUN NTH (LAMBDA (N LST)
; Функция возвращает N-й элемент списка LST ;
(COND ( (EQ N 1) (CAR LST) )
( T (NTH (- N 1) (CDR LST)) )
)
))
Тестовые примеры:
$ (NEIGHBOUR1 2 '((0 1 1 0) (0 0 1 0) (0 0 0 1) (1 0 0 0))) (3) $ (NEIGHBOUR1 1 '((0 1 1 0) (0 0 1 0) (0 0 0 1) (1 0 0 0))) (2 3) $ (NEIGHBOUR1 4 '((0 1 1 0) (0 0 1 0) (0 0 0 1) (1 0 0 0))) (1)
Достаточно очевидно, что рассмотренная в программе реализация матрицы смежности с помощью S-выражения весьма неэффективна. Основным ее недостатком является отсутствие прямого доступа к элементам матрицы (в некоторых диалектах языка LISP). В следующих шагах разделе мы усовершенствуем это представление!
Замечания.
- Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одинаковыми перестановками строк и столбцов [1, с.28].
- В теории графов классическим способом представления графа
служит матрица инцидентности [2, с.84-85]. Это матрица A с
N строками, соответствующими вершинам, и M столбцами, соответствующими ребрам.
Для ориентированного графа, столбец соответствующий дуге <x,y>, принадлежащей E, содержит -1 в строке, соответствующей вершине x, 1 в строке, соответствующей вершине y, и нули во всех остальных строках (петлю, т.е. дугу вида <x,x>, удобно представлять иным значением в строке x, например, 2).
В случае неориентированного графа столбец, соответствующий ребру {x,y}, содержит 1 в строках, соответствующих x и y, а нули в остальных строках.
С алгоритмической точки зрения матрица инцидентности является, вероятно, самым худшим способом представления графа, который только только можно себе представить.
Этот способ требует NxM ячеек памяти, причем большинство этих ячеек вообще занято нулями. Неудобен также доступ к информации. Ответ на элементарные вопросы типа "существует ли дуга <x,y>?", "к каким вершинам ведут ребра из x?" требует в худшем случае перебора всех столбцов матрицы, а следовательно, M шагов.
- Графы (ориентированные графы) изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга произвольными перестановками строк и столбцов [1, с.28].
- Существуют еще несколько способов представления графов с помощью матриц:
- матрица достижимости (для ее построения используется алгоритм Уоршалла) [3, с.439],
- матрица циклов [4, с.183-186],
- матрица Кирхгофа [1, с.30-31].
(1)Лекции по теории графов / Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. - М.: Наука, 1990. - 384 с.
(2)Липский В. Комбинаторика для программистов: Пер. с польск. - М.: Мир, 1988. - 213 с.
(3) Траамбле Ж., Соренсон П. Введение в структуры данных. - М.: Машиностроение, 1982. - 784 с.
(4)Харари Ф. Теория графов. - М.: Мир, 1973. - 300 с.
На следующем шаге мы рассмотрим использование структур смежности для представления графов.
