На этом шаге мы рассмотрим использование структур смежности для представления графов.
Более экономным в отношении памяти (особенно в случае неплотных графов, когда M гораздо меньше NxN) является метод представления графа с помощью так называемой структуры смежности, представляющей собой в простейшем случае список пар, соответствующих его ребрам. Пара <x,y> соответствует дуге <x,y>, если граф ориентированный, и ребру {x,y} в случае неориентированного графа.
Например, приведем списки ребер, соответствующие графам:
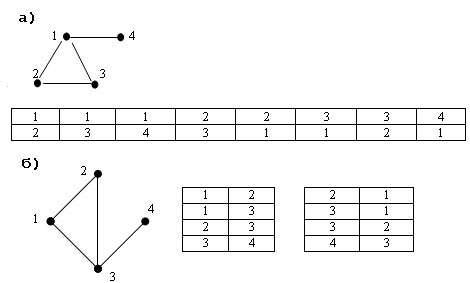
Рис.1. Списки ребер
Очевидно, что объем памяти в этом случае составляет 2xM. Неудобством является большое число шагов (порядка M в худшем случае), необходимое для получения множества вершин, к которым ведут ребра из данной вершины.
Ситуацию можно значительно улучшить, упорядочив множество пар лексикографически и применяя двоичный поиск, но лучшим решением во многих случаях оказывается структура данных, которую мы будем называть списками инцидентности. Она содержит для каждой вершины v из V список смежных ей вершин. Точнее, каждый элемент такого списка является записью R, содержащей вершину R.Строка и указатель R.След на следующую запись в списке (R.След=Nil для последней записи в списке).
Указатель НАЧАЛО[v] является указателем на начало списка, содержащего вершины из множества вершин, смежных с данной вершиной v.
Отметим, что для неориентированных графов каждое ребро представлено в списках инцидентности дважды.
Приведем пример представления неориентированного графа с посощью списков инцидентности (N обозначает Nil):
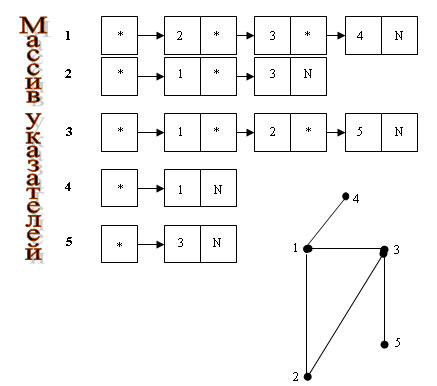
Рис.2. Представление неориентированного графа
Во многих алгоритмах структура графа динамически модифицируется добавлением и удалением ребер. В таких случаях полагаем, что в наших списках инцидентности элемент списка НАЧАЛО[u], содержащий вершину v, снабжен указателем на элемент списка НАЧАЛО[v], содержащий вершину u, и что каждый элемент списка содержит указатель не только к следующему элементу, но и к предыдущему. Тогда, удаляя некоторый элемент из списка, мы можем легко за число шагов, ограниченное константой, удалить другой элемент, представляющий то же самое ребро, не просматривая список, содержащий этот элемент.
Число ячеек памяти, необходимое для представления графа с помощью списков инцидентности, будет, очевидно, иметь порядок M+N.
Представление структуры смежности в виде списка ребер - простейший способ представления графа на языке LISP. Такой список естественно реализовать как список, состоящий из точечных пар смежных вершин. Однако при таком подходе следует специально позаботиться о вершинах, не соединенных с другими вершинами посредством ребер. Можно, например, для изображения таких "одиноких" вершин добавлять к списку ребер фиктивное ребро, соединяющее "одинокую" вершину с вершиной FALSE.
В качестве примеров использования способа представления графа в виде списка ребер построим:
- функцию, которая в ориентированном графе GRAPH находит
список соседей вершины X (т.е. вершин, соединенных с ней хотя бы одним ребром):
Текст этой программы можно взять здесь.
(DEFUN NEIGHBOUR2 (LAMBDA (X GRAPH) (COND ( (NULL GRAPH) NIL ) ( (AND (EQ (CAAR GRAPH) X) (EQ (CDAR GRAPH) FALSE)) NIL ) ( (EQ (CAAR GRAPH) X) (CONS (CDAR GRAPH) (NEIGHBOUR2 X (CDR GRAPH))) ) ( (EQ (CDAR GRAPH) X) (CONS (CAAR GRAPH) (NEIGHBOUR2 X (CDR GRAPH))) ) ( T (NEIGHBOUR2 X (CDR GRAPH)) ) ) ))Тестовые примеры:
$ (NEIGHBOUR2 2 '((1 . 2) (1 . 3) (2 . 3) (5 . FALSE))) (1 3) $ (NEIGHBOUR2 1 '((1 . 2) (1 . 3) (2 . 3) (5 . FALSE))) (2 3) $ (NEIGHBOUR2 5 '((1 . 2) (1 . 3) (2 . 3) (5 . FALSE))) NIL
- функцию, которая в неориентированном графе GRAPH находит список соседей вершины X (т.е. вершин, соединенных с ней
хотя бы одним ребром):
Текст этой программы можно взять здесь.
(DEFUN MAIN (LAMBDA (X GRAPH) (LIST-SET (NEIGHBOUR2 X GRAPH)) )) ; ------------------------------- ; (DEFUN NEIGHBOUR2 (LAMBDA (X GRAPH) (COND ( (NULL GRAPH) NIL ) ( (AND (EQ (CAAR GRAPH) X) (EQ (CDAR GRAPH) 'FALSE)) NIL ) ( (EQ (CAAR GRAPH) X) (CONS (CDAR GRAPH) (NEIGHBOUR2 X (CDR GRAPH))) ) ( (EQ (CDAR GRAPH) X) (CONS (CAAR GRAPH) (NEIGHBOUR2 X (CDR GRAPH))) ) ( T (NEIGHBOUR2 X (CDR GRAPH)) ) ) )) ; ------------------------- ; (DEFUN LIST-SET (LAMBDA (LST) ; Функция LIST-SET преобразует список LST в список, в ко-; ; тором каждый элемент встречается лишь по одному разу ; (COND ( (NULL LST) NIL ) ( (MEMBER (CAR LST) (CDR LST)) (LIST-SET (CDR LST)) ) ( T (CONS (CAR LST) (LIST-SET (CDR LST))) ) ) ))Тестовые примеры:
$ (MAIN 2 '((1 . 2) (1 . 3) (2 . 3) (2 . 1) (3 . 1) (3 . 2) (5 . FALSE))) (1 3) $ (MAIN 1 '((1 . 2) (1 . 3) (2 . 3) (2 . 1) (3 . 1) (3 . 2) (5 . FALSE))) (2 3) $ (MAIN 5 '((1 . 2) (1 . 3) (2 . 3) (2 . 1) (3 . 1) (3 . 2) (5 . FALSE))) NIL
Ясно, что при представлении графа в виде списка ребер информация о вершинах может оказаться труднодоступной. Так будет в случае, когда число ребер намного больше числа вершин.
Cамым удобным представлением графов в языке LISP является представление структуры смежности в виде ассоциативного списка. Первый элемент точечной пары, входящей в этот список, представляет собой вершину графа. Второй же элемент - это список вершин, соседних с данной.
Приведем примеры представления структуры смежности в виде ассоциативного списка:
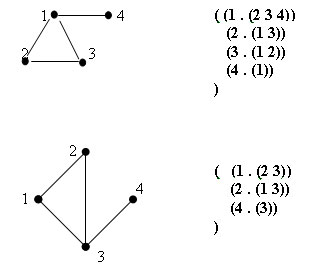
Рис.3. Представление в виде ассоциативного списка
Теперь задача о поиске всех соседей данной вершины решается совсем просто [1, с.127]:
(DEFUN NEIGHBOUR3 (LAMBDA (X GRAPH)
(COND ( (NULL (ASSOC X GRAPH)) NIL )
( T (CDR (ASSOC X GRAPH)) )
)
))
Тестовые примеры:
$ (NEIGHBOUR3 2 ' ((1 . (2 3 4)) (2 . (1 3)) (3 . (1 2)) (4 . (1)))) (1 3) $ (NEIGHBOUR3 1 ' ((1 . (2 3 4)) (2 . (1 3)) (3 . (1 2)) (4 . (1)))) (2 3 4) $ (NEIGHBOUR3 3 ' ((1 . (2 3 4)) (2 . (1 3)) (3 . (1 2)) (4 . (1)))) (1 2)
(1) Крюков А.П., Радионов А.Я., Таранов А.Ю., Шаблыгин Е.М. Программирование на языке R-Лисп. - М.: Радио и связь, 1991. - 192 с.
На следующем шаге мы разберем представление графов с помощью динамических структур.
