На этом шаге мы рассмотрим алгоритм поиска в глубину.
Два наиболее распространенных алгоритма поиска на графе называются "поиск в глубину" и "поиск в ширину". Первый из них основан на таком порядке просмотра вершин графа, когда новая вершина, покуда это возможно, выбирается среди соседей текущей вершины. Если среди соседей текущей вершины нет таких, что не были просмотрены ранее, мы возвращаемся к предыдущей вершине и возобновляем поиск.
Программа, реализующая этот алгоритм, выглядит следующим образом [1, с.128]:
(DEFUN DEPTHFIRST (LAMBDA (GRAPH ROOT) ; GRAPH - граф, заданный в виде структуры смежности ; ; ROOT - вершина графа, с которой начинается поиск ; ; Результат: список вершин графа в порядке прохождения ; (COND ( (NULL GRAPH) NIL ) ( T (DEFI GRAPH (LIST ROOT) (LIST ROOT)) ) ) )) ; ------------------------------------ ; (DEFUN DEFI (LAMBDA (GRAPH VISITED PATH) ; VISITED - список уже просмотренных вершин ; ; PATH - список вершин, определяющих путь просмотра ; (COND ( (NULL PATH) (REVERSE VISITED) ) ( T (COND ( (NULL (EXPND GRAPH VISITED (CAR PATH))) (DEFI GRAPH VISITED (CDR PATH)) ) ( T (DEFI GRAPH (CONS (EXPND GRAPH VISITED (CAR PATH)) VISITED) (CONS (EXPND GRAPH VISITED (CAR PATH)) PATH)) )) ) ) )) ; --------------------------------------- ; (DEFUN EXPND (LAMBDA (GRAPH VISITED VERTEX) ; Выбор следующей еще не просмотренной вершины соседней ; ; с VERTEX ; (COND ( (NULL (NEIGHBOUR3 VERTEX GRAPH)) NIL ) ( T (FIRSTNOTVISITED VISITED (NEIGHBOUR3 VERTEX GRAPH)) ) ) )) ; ------------------------------------------ ; (DEFUN FIRSTNOTVISITED (LAMBDA (VISITED VLIST) (COND ( (NULL VLIST) NIL ) ( T (COND ( (NULL (MEMBER (CAR VLIST) VISITED)) (CAR VLIST) ) ( T (FIRSTNOTVISITED VISITED (CDR VLIST)) )) ) ) )) ; ------------------------------- ; (DEFUN NEIGHBOUR3 (LAMBDA (X GRAPH) (COND ( (NULL (ASSOC X GRAPH)) NIL ) ( T (CDR (ASSOC X GRAPH)) ) ) ))
Тестовые примеры:
$ (DEPTHFIRST '((1 . (2 3 4)) (2 . (3)) (3 . (4))) 1) (1 2 3 4) $ (DEPTHFIRST '((1 . (2 3 4)) (2 . (3)) (3 . (4))) 2) (2 3 4) $ (DEPTHFIRST '((1 . (2 3 4)) (2 . (3)) (3 . (4))) 3) (3 4) $ (DEPTHFIRST '((1 . (2 3 4)) (2 . (3 1)) (3 . (4))) 2) (2 3 4 1) $ (DEPTHFIRST '((1 . (2 3)) (2 . (4 5)) (3 . (6 7))) 1) (1 2 4 5 3 6 7)
Последний тестовый пример иллюстрируется следующим графом:
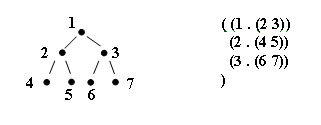
Рис.1. Пример графа
Программа работает следующим образом.
Если граф не пуст, то в два списка: VISITED - список уже просмотренных вершин и PATH - список вершин, определяющих путь просмотра, заносится первая вершина графа. После этого вызывается функция DEFI. Ее третий аргумент - список PATH - позволяет нам в любой момент вернуться к предыдущей вершине. Список VISITED используется для того, чтобы помнить о том, какие вершины уже пройдены. Выбор следующей вершины осуществляется с помощью функции EXPND. Именно работой этой функции определяется порядок просмотра графа. В нашем случае, пока возможно, для просмотра выбирается соседняя вершина, т.е. на каждом шаге алгоритма делается попытка пройти вглубь графа. В противном случае из списка PATH удаляется первый элемент, и поиск возобновляется с предыдущей вершины.
Значением функции DEPTHFIRST является список вершин графа в том порядке, в котором эти вершины были просмотрены. Очевидно, что этот порядок зависит от вершины, с которой просмотр начинается. Более того, для некоторых графов списки просмотренных вершин, полученные при различных значениях начальной вершины, вообще не имеют ни одного общего элемента.
Мы уже упоминали о том, что параметр PATH функции DEFI описывает путь из начальной вершины в просматриваемую. Поэтому алгоритм поиска вершины можно легко модифицировать в алгоритм поиска пути между заданными вершинами (например, вершинами ROOT и END):
(DEFUN WAY (LAMBDA (GRAPH ROOT END)
(COND ( (NULL GRAPH) NIL )
( T (DEFI GRAPH (LIST ROOT) (LIST ROOT) END) )
)
))
; ---------------------------------------- ;
(DEFUN DEFI (LAMBDA (GRAPH VISITED PATH END)
; VISITED - список уже просмотренных вершин ;
; PATH - список вершин, определяющих путь просмотра ;
; END - конечная вершина пути ;
(COND ( (NULL PATH) (REVERSE VISITED) )
( T (COND ( (NULL (EXPND GRAPH VISITED (CAR PATH)))
(DEFI GRAPH VISITED (CDR PATH) END)
)
( (EQ (EXPND GRAPH VISITED (CAR PATH)) END)
(REVERSE (CONS END PATH)) )
( T (DEFI GRAPH
(CONS (EXPND GRAPH VISITED
(CAR PATH))
VISITED)
(CONS (EXPND GRAPH VISITED
(CAR PATH))
PATH)
END) )) )
)
))
; --------------------------------------- ;
(DEFUN EXPND (LAMBDA (GRAPH VISITED VERTEX)
; Выбор следующей еще не просмотренной вершины ;
; соседней с VERTEX ;
(COND ( (NULL (NEIGHBOUR3 VERTEX GRAPH)) NIL )
( T (FIRSTNOTVISITED
VISITED
(NEIGHBOUR3 VERTEX GRAPH))
)
)
))
; ------------------------------------------ ;
(DEFUN FIRSTNOTVISITED (LAMBDA (VISITED VLIST)
(COND ( (NULL VLIST) NIL )
( T (COND ( (NULL (MEMBER (CAR VLIST) VISITED))
(CAR VLIST)
)
( T (FIRSTNOTVISITED
VISITED
(CDR VLIST))
)
)
)
)
))
; ------------------------------- ;
(DEFUN NEIGHBOUR3 (LAMBDA (X GRAPH)
(COND ( (NULL (ASSOC X GRAPH)) NIL )
( T (CDR (ASSOC X GRAPH)) )
)
))
Тестовые примеры:
$ (WAY '((1 . (2)) (2 . (3 4)) (3 . ()) (4 . (5)) (5 . (2 7 8)) (7 . ()) (8 . ())) 1 2) (1 2) $ (WAY '((1 . (2)) (2 . (3 4)) (3 . ()) (4 . (5)) (5 . (2 7 8)) (7 . ()) (8 . ())) 1 5) (1 2 4 5) $ (WAY '((1 . (2)) (2 . (3 4)) (3 . ()) (4 . (5)) (5 . (2 7 8)) (7 . ()) (8 . ())) 4 2) (4 5 2) $ (WAY '((1 . (2)) (2 . (3 4)) (3 . ()) (4 . (5)) (5 . (2 7 8)) (7 . ()) (8 . ())) 7 7) (7) $ (WAY '((1 . (2)) (2 . (3 4)) (3 . ()) (4 . (5)) (5 . (2 7 8)) (7 . ()) (8 . ())) 1 1) (1 2 3 4 5 7 8)
Замечания.
- Алгоритм поиска в глубину на графе изложен, например, в монографиях [2, с.198-205], [3, с.88-91].
- В приведенной ниже формулировке нерекурсивного алгоритма поиска в глубину на графе [4, с.125-126] предполагается, во-первых, что зафиксирован некоторый линейный порядок на множестве всех вершин графа, и, во-вторых, что множество вершин, смежных со всякой вершиной графа, также линейно упорядочено:
WHILE Имеется хотя бы одна непосещенная вершина DO BEGIN Пусть p - первая (т.е. минимальная) из непосещенных вершин. Посетить вершину p и поместить ее в пустой стек S; WHILE Стек S непуст DO BEGIN Пусть p - вершина, находящаяся на верхушке стека S; IF У вершины p есть непосещенные смежные вершины THEN BEGIN Пусть q - первая непосещенная вершина из вершин, смежных вершине p. Пройти по ребру (p,q), посетить вер- шину q и поместить ее в стек S END ELSE Удалить вершину p из стека S END END
В результате работы алгоритма пройденные ребра графа образуют вместе с посещенными вершинами одно или несколько деревьев. Если приписать пройденным ребрам ориентацию в соответствии с тем направлением, в каком они проходятся при выполнении алгоритма, то мы получим совокупность корневых деревьев, причем их корнями будут служить те вершины, которые в процессе работы алгоритма помещались в пустой стек.
(1) Крюков А.П., Радионов А.Я., Таранов А.Ю., Шаблыгин Е.М. Программирование на языке R-Лисп. - М.: Радио и связь, 1991. - 192 с.
(2) Пападимитриу Х., Стайнглиц К. Комбинаторная оптимизация. - М.: Мир, 1985. - 512 с.
(3) Липский В. Комбинаторика для программистов: Пер. с польск. - М.: Мир, 1988. - 213 с.
(4) Касьянов В.Н., Сабельфельд В.К. Сборник заданий по практикуму на ЭВМ. - М.: Наука, 1986. - 272 с.
На следующем шаге мы рассмотрим поиск в ширину.
