На этом шаге мы рассмотрим алгоритм поиска в ширину.

Перейдем теперь к другому алгоритму поиска на графе, известному под названием поиск в ширину. При поиске в ширину сначала просматриваются все соседи текущей вершины и только после этого происходит продвижение по графу. Таким образом поиск ведется как бы во всех возможных направлениях одновременно [1, с.131]:

   (DEFUN BREADTHFIRST (LAMBDA (GRAPH ROOT)
   ; GRAPH - граф в виде структуры смежности              ;
   ; ROOT  - вершина графа, с которой начинается поиск    ;
   ; Результат: список вершин графа в порядке прохождения ;
      (BRFI
         GRAPH
         (LIST ROOT)
         (NEIGHBOUR3 ROOT GRAPH)
      )
   ))
   ; ------------------------------------- ;
   (DEFUN BRFI (LAMBDA (GRAPH VISITED QUEUE)
   ; VISITED - список уже просмотренных вершин     ;
   ; QUEUE   - очередь вершин, ожидающих просмотра ;
      (COND ( (NULL QUEUE) (REVERSE VISITED) )
            ( T (COND ( (MEMBER (CAR QUEUE) VISITED)
                           (BRFI
                              GRAPH
                              VISITED
                              (CDR QUEUE)) )
                      (  T  (BRFI
                               GRAPH
                               (CONS (CAR QUEUE) VISITED)
                               (APPEND
                                  QUEUE
                                  (NEIGHBOUR3 (CAR QUEUE)
                                              GRAPH))) )) )
      )
   ))
   ; ------------------------------- ;
   (DEFUN NEIGHBOUR3 (LAMBDA (X GRAPH)
      (COND ( (NULL (ASSOC X GRAPH)) NIL )
            (  T  (CDR (ASSOC X GRAPH)) )
      )
   ))

Текст этой библиотеки можно взять здесь.

Тестовый пример:

   $ (SETQ G '((1 .  (2 3 4)) (2 . (1 3)) (3 . (1 2 4))
   (4 . (1 3 5)) (5 . (4))))
   ((1 . (2 3 4)) (2 . (1 3)) (3 . (1 2 4)) (4 . (1 3 5))
   (5 . (4)))
   $ (BREADTHFIRST G 4)
   (4 1 3 5 2)
   $ (BREADTHFIRST '((1 . (2 3 4)) (2 . (3)) (3 . (4))) 1)
   (1 2 3 4)
   $ (BREADTHFIRST '((1 . (2 3 4)) (2 . (3)) (3 . (4))) 2)
   (2 3 4)
   $ (BREADTHFIRST '((1 . (2 3 4)) (2 . (3)) (3 . (4))) 3)
   (3 4)
   $ (BREADTHFIRST '((1 . (2 3 4)) (2 . (3 1)) (3 . (4))) 2)
   (2 3 1 4)
   $ (BREADTHFIRST '((1 . (2 3)) (2 . (4 5)) (3 . (6 7))) 1)
   (1 2 3 4 5 6 7)

Последний тестовый пример иллюстрируется следующим графом:

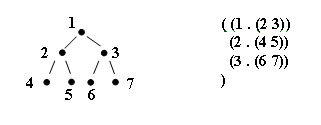
Рис.1. Пример графа

Мы видим, что при поиске в ширину ближайшие соседи последней просмотренной вершины добавляются в конец списка QUEUE, в то время как новые вершины для просмотра берутся из начала этого списка, т.е. параметр QUEUE представляет собой очередь в отличие от параметра PATH функции DEFI, который работает как стек. Это приводит к тому, что в процессе работы функции BRFI просмотренные вершины в списке VISITED расположены в порядке невозрастания их расстояния от начальной вершины ROOT.

Замечания.

Алгоритм поиска в ширину на графе изложен, например, в монографиях [2, с.198-205], [3, с.88-91].
Способ обхода деpева в шиpину, называемый иногда способом пpохождения в гоpизонтальном поpядке, основан на посещении узлов деpева слева напpаво, уpовень за уpовнем вниз от коpня.
Пpиведенный ниже нерекурсивный алгоpитм pеализует обход деpева в шиpину, используя две очеpеди O1 и O2 [4, с.124 -125]:
Взять пустые очеpеди O1 и O2. Поместить коpень в очеpедь O1. WHILE Одна из очеpедей O1 и O2 не пуста DO IF O1 не является пустой THEN BEGIN Пусть p - узел, находящийся в голове очеpеди O1. Посетить веpшину p и удалить ее из O1. Поместить всех сыновей веpшины p в очеpедь O2, начиная со стаpшего сына END ELSE В качестве O1 взять непустую очеpедь O2, а в качестве O2 взять пустую очеpедь O1.

⁽¹⁾ Крюков А.П., Радионов А.Я., Таранов А.Ю., Шаблыгин Е.М. Программирование на языке R-Лисп. - М.: Радио и связь, 1991. - 192 с.
⁽²⁾ Пападимитриу Х., Стайнглиц К. Комбинаторная оптимизация. - М.: Мир, 1985. - 512 с.
⁽³⁾ Липский В. Комбинаторика для программистов: Пер. с польск. - М.: Мир, 1988. - 213 с.
⁽⁴⁾ Касьянов В.Н., Сабельфельд В.К. Сборник заданий по практикуму на ЭВМ. - М.: Наука, 1986. - 272 с.

Со следующего шага мы начнем рассматривать примеры алгоритмов на графах .

Предыдущий шаг Содержание Следующий шаг