На этом шаге мы рассмотрим общую схему решения системы линейных уравнений методом Гаусса.

Линейное уравнение с n неизвестными x₀, x₁, ..., x_n-1 может быть определено при помощи выражения a₀x₀+ a₁x₁+ … + a_n-1x_n-1= b, где величины a₀, a₁, ..., a_n-1 и b представляют собой постоянные значения.

Множество n линейных уравнений

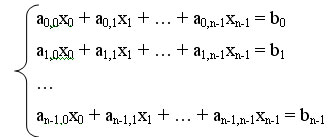
называется системой линейных уравнений или линейной системой. В более кратком (матричном) виде система может быть представлена как Ax = b, где A=(a_i,j) есть вещественная матрица размера n*n, а векторы b и x состоят из n элементов.

Под задачей решения системы линейных уравнений для заданных матрицы А и вектора b обычно понимается нахождение значения вектора неизвестных x, при котором выполняются все уравнения системы.

Последовательные алгоритмы. Алгоритм Гаусса

Если система линейных уравнений является невырожденной, то метод Гаусса гарантирует нахождение решения с погрешностью, определяемой точностью машинных вычислений. Основная идея метода состоит в приведении матрицы А посредством эквивалентных преобразований к треугольному виду, после чего значения искомых неизвестных может быть получено непосредственно в явном виде. К числу эквивалентных преобразований относятся:

умножение любого из уравнений на ненулевую константу,
перестановка уравнений,
прибавление к уравнению любого другого уравнения системы.

Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе - прямой ход метода Гаусса - исходная система линейный уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду Ux = c, где матрица коэффициентов получаемой системы имеет вид

На обратном ходе метода Гаусса (второй этап алгоритма) осуществляется определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной x_n-1, после этого из предпоследнего уравнения становится возможным определение переменной x_n-2 и т.д.

Прямой ход алгоритма Гаусса

Прямой ход метода Гаусса состоит в последовательном исключении неизвестных в уравнениях решаемой системы линейных уравнений. На итерации i, 0<=i<n-1, метода производится исключение неизвестной i для всех уравнений с номерами k, больших i (т.е. i<k<=n-1). Для этого из этих уравнений осуществляется вычитание строки i, умноженной на константу (a_ki/a_ii) c тем, чтобы результирующий коэффициент при неизвестной x_i в строках оказался нулевым - все необходимые вычисления могут быть определены при помощи соотношений:

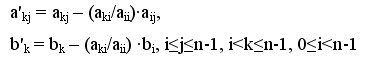
(при этом аналогичные вычисления выполняются и над вектором b).

При выполнении прямого хода метода Гаусса строка, которая используется для исключения неизвестных, носит наименование ведущей, а диагональный элемент ведущей строки называется ведущим элементом. Ясно, что выполнение вычислений является возможным только тогда, когда ведущий элемент имеет ненулевое значение. Более того, если ведущий элемент a_i,i имеет малое значение, то деление и умножение строк на этот элемент может приводить к накоплению вычислительной погрешности и вычислительной неустойчивости алгоритма.

Возможный способ избежать подобной проблемы может состоять в следующем - при выполнении каждой очередной итерации прямого хода метода Гаусса следует определить коэффициент с максимальным значением по абсолютной величине в столбце, соответствующем исключаемой неизвестной, т.е.

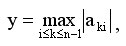
и выбрать в качестве ведущей строку, в которой этот коэффициент располагается (данная схема выбора ведущего значения носит наименование метода главных элементов).

Вычислительная сложность прямого хода алгоритма Гаусса с выбором ведущей строки имеет порядок O(n³).

Обратный ход алгоритма Гаусса

После приведения матрицы коэффициентов к верхнему треугольному виду становится возможным определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной x_n-1, после этого из предпоследнего уравнения становится возможным определение переменной x_n-2 и т.д. В общем виде, выполняемые вычисления при обратном ходе метода Гаусса могут быть представлены при помощи соотношений:

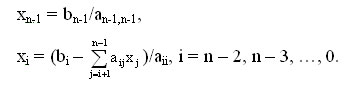
На следующем шаге мы продолжим изучение этого вопроса.

Предыдущий шаг Содержание Следующий шаг