На этом шаге мы рассмотрим метод сопряженных градиентов.

Метод сопряженных градиентов

Рассмотрим теперь совершенно иной подход к решению систем линейных уравнений, при котором к искомому точному решению x* системы Ax=b строится последовательность приближенных решений x⁰, x¹, ..., x^k,... При этом процесс вычислений организуется таким способом, что каждое очередное приближение дает оценку точного решения со все уменьшающейся погрешностью, и при продолжении расчетов оценка точного решения может быть получена с любой требуемой точностью. К преимуществам подобных итерационных методов можно отнести меньший объем (по сравнению, например, с методом Гаусса) необходимых вычислений для решения разреженных систем линейных уравнений, возможность более быстрого получения начальных приближений искомого решения, наличие эффективных способов организации параллельных вычислений.

Одним из наиболее известных итерационных алгоритмов является метод сопряженных градиентов, который может быть применен для решения симметричной положительно определенной системы линейных уравнений большой размерности.

Напомним, что матрица А является симметричной, если она совпадает со своей транспонированной матрицей, т.е. А=А^Т. Матрица А называется положительно определенной, если для любого вектора x справедливо: x^TAx>0.

Известно, что после выполнения n итераций алгоритма (n есть порядок решаемой системы линейных уравнений) очередное приближение xⁿ совпадает с точным решением.

Последовательный алгоритм

Если матрица А симметричная и положительно определенная, то функция

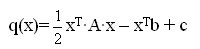
имеет единственный минимум, который достигается в точке x*, совпадающей с решением системы линейных уравнений. Метод сопряженных градиентов является одним из широкого класса итерационных алгоритмов, которые позволяют найти решение путем минимизации функции q(x).

Итерация метода сопряженных градиентов состоит в вычислении очередного приближения к точному решению в соответствии с правилом:

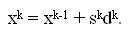
Тем самым, новое значение приближения x^k вычисляется с учетом приближения, построенного на предыдущем шаге x^k-1, скалярного шага s^k и вектора направления d^k.

Перед выполнением первой итерации вектора x⁰ и d⁰ полагаются равными нулю, а для вектора g⁰ устанавливается значение равное -b. Далее каждая итерация для вычисления очередного значения приближения x_k включает выполнение четырех шагов:

Шаг 1. Вычисление градиента:

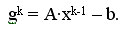
Шаг 2. Вычисление вектора направления:

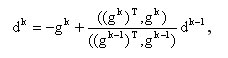
где (g^T,g) есть скалярное произведение векторов.

Шаг 3. Вычисление величины смещения по выбранному направлению:

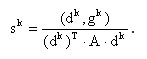
Шаг 4. Вычисление нового приближения:

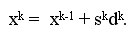
Как можно заметить, данные выражения включают две операции умножения матрицы на вектор, четыре операции скалярного произведения и пять операций над векторами. Как результат, что общее количество числа операций, выполняемых на одной итерации, составляет

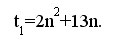
Для нахождения точного решения системы линейных уравнений с положительно определенной симметричной матрицей необходимо выполнить n итераций. Таким образом, для нахождения решения системы необходимо выполнить

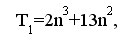
и, тем самым, сложность алгоритма имеет порядок O(n³).

На следующем шаге мы продолжим изучение этого вопроса.

Предыдущий шаг Содержание Следующий шаг