На этом шаге мы разберемся с линейной регрессией.

Линейная регрессия - наиболее часто встречающийся в начальных руководствах по машинному обучению алгоритм. Он часто применяется для решения задач регрессии, в которых модель предсказывает отсутствующие значения данных на основе имеющихся. Немаловажное преимущество линейной регрессии как для преподавателей, так и и для тех, кто ею пользуется, - ее простота. Что, впрочем, отнюдь не означает, что с ее помощью нельзя решать реальные задачи! У линейной регрессии множество сценариев применения на практике в самых разнообразных сферах, например исследованиях рынка, астрономии и биологии. На этом шаге вы узнаете все, что нужно для начала работы с линейной регрессией.

Общее описание

Как с помощью линейной регрессии предсказать курс акций в заданный день? Прежде чем ответить на этот вопрос, приведем несколько определений.

Любая модель машинного обучения состоит из параметров модели. Параметры модели - внутренние переменные ее конфигурации, оцениваемые на основе имеющихся данных. Эти параметры модели определяют вычисленнные моделью предсказания по заданным входным признакам. В случае линейной регрессии параметры модели называются коэффициентами. Наверное, вы помните из школьного курса формулу прямой на плоскости: f(x) = kx + b. Переменные k и b - коэффициенты линейного уравнени. Оно описывает преобразование каждого из входных сигналов x в выходной сигнал f(x), так что все выходные сигналы вместе описывают прямую на плоскости. Меняя коэффициенты, можно описать любую прямую в двумерном пространстве.

Модель линейной регрессии сочетает заданные входные признаки x₁, x₂, ..., x_k с коэффициентами a₁, a₂,..., a_k для вычисления предсказываемого выходного сигнала у по формуле:

  у = f(x) = a₀ + a₁ × x₁ + a₂ × x₂ + ... + a_k × x_k   .

В нашем примере с курсами акций один входной признак: x - день. Мы подаем на вход день x в надежде получить курс акций, то есть выходной сигнал у. Что упрощает модель линейной регрессии до формулы прямой на плоскости:

  y = f(x) = a₀ + a₁x   .

Посмотрим на три прямые, отличающиеся только двумя параметрами модели a₀ и a₁ на рисунке 1.

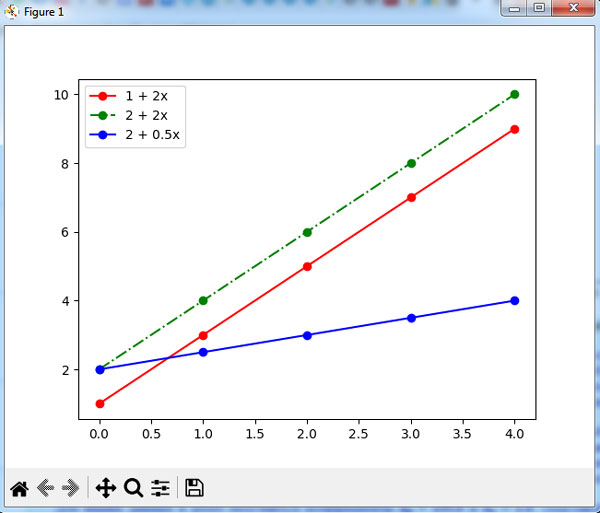
Рис.1. Три модели (прямые) линейной регрессии, соответствующие различным параметрам (коэффициентам) модели. Каждая из этих прямых отражает взаимосвязь между входной и выходной величинами

Первая ось координат отражает входной сигнал x. Вторая - выходной сигнал у. Прямые отражают (линейную) связь между входным и выходным сигналами.

Пусть в нашем примере с курсами акций обучающие данные представляют собой индексы для трех дней, [0, 1, 2], соответствующие курсам акций [155, 156, 157]. Другими словами:

входной сигнал x = 0 должен приводить к выходному сигналу у = 155;
входной сигнал x = 1 должен приводить к выходному сигналу у = 156;
входной сигнал x = 2 должен приводить к выходному сигналу у = 157.

Какая же прямая хорошо соответствует нашим обучающим данным? Мы отобразили обучающие данные на рисунке 2.

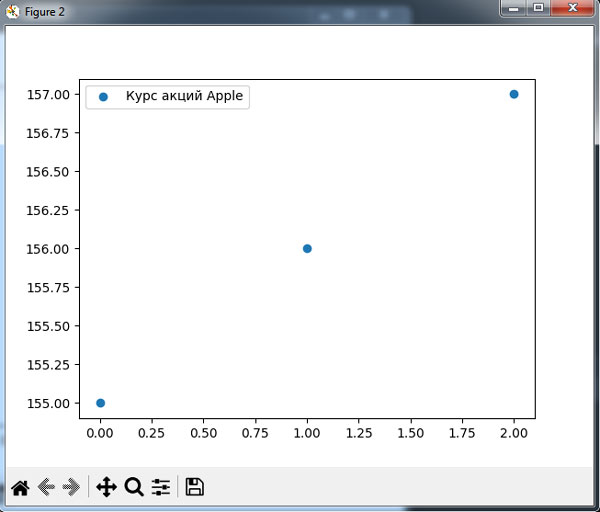
Рис.2. Наши обучающие данные с индексом в массиве в качестве координаты x и ценой в качестве координаты y

Чтобы найти прямую, лучше всего описывающую наши данные, а значит, лучшую и для создания модели линейной регрессии, необходимо определить коэффициенты. Именно для этого и служит машинное обучение. Существует два основных способа определения параметров модели для линейной регрессии. Во-первых, можно аналитически вычислить лучше всего подходящую прямую между этими точками (стандартный подход для линейной регрессии).

Во-вторых, можно пробовать различные модели, проверяя каждую на маркированной выборке данных, и в конце концов найти лучшую. В любом случае "лучшая" модель выбирается путем минимизации погрешности (error minimization), при которой модель минимизирует квадрат разности (выбирает минимизирующие ее коэффициенты) предсказанных моделью значений и идеального выходного сигнала, выбирая модель с самой низкой погрешностью.

Для наших данных в итоге получаются коэффициенты а₀ = 155.0 и а₁ = 1.0. Подставляем их в нашу формулу линейной регрессии:

  y = f(x) = a₀ + a₁x = 155.0 + 1.0 × x

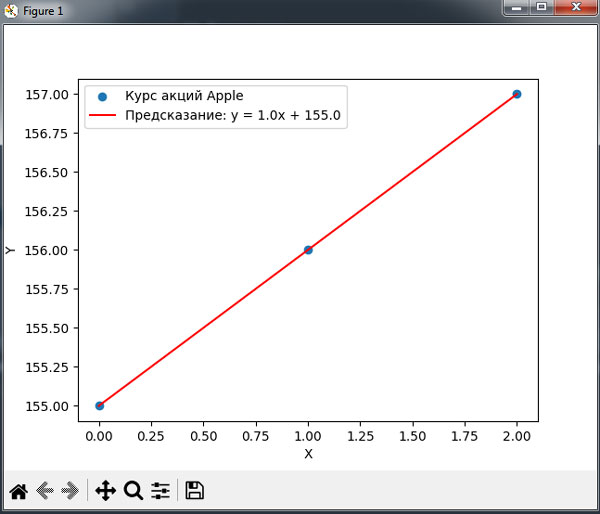
и строим на одном графике прямую и добавляем обучающие данные, как показано на рисунке 3.

Рис.3. Прямая предсказания на основе нашей модели линейной регрессии

Идеально! Квадрат расстояния между прямой (прогнозом модели) и обучающими данными равен нулю - мы нашли модель, которая минимизирует погрешность. С помощью этой модели теперь можно предсказывать курсы акций для любых значений х. Например, пусть мы хотим предсказать курс акций в день х = 4. Для этого мы просто можем воспользоваться моделью и вычислить f(x) = 155.0 + 1.0 × 4 = 159.0. Итак, предсказанный курс акций на четвертый день равен 159 долларам. Конечно, совсем другое дело, насколько хорошо это предсказание отражает реальность.

Такова общая картина происходящего. Теперь посмотрим на то, как выглядит соответствующий код.

На следующем шаге мы закончим изучение этого вопроса.

Предыдущий шаг Содержание Следующий шаг